"एक्सरे और मणिभ संरचना": अवतरणों में अंतर
(''''एक्सरे और मणिभ संरचना''' द्रव्य की संरचना के अध्ययन...' के साथ नया पृष्ठ बनाया) |
आदित्य चौधरी (वार्ता | योगदान) छो (Text replacement - "सरंचना" to "संरचना") |
||
| पंक्ति 1: | पंक्ति 1: | ||
'''एक्सरे और मणिभ संरचना''' द्रव्य की संरचना के अध्ययन में एक्सरे का विशेष स्थान है। द्रव्य के चरम रचक परमाणु हैं। परमाणुओं का आकार अत्यंत सूक्ष्म होता है, अत: उनके अध्ययन के लिए अत्यंत सूक्ष्म प्रकार के साधनों की आवश्यकता होती है। प्रकाश का तरंगदैर्घ्य परमाणुओं के आकार से बहुत अधिक होने के कारण संरचनात्मक अध्ययन में प्रकाश का विशेष उपयोग नहीं हो सकता। एक्सरे का तरंगदैर्ध्य 1 ऐंगस्ट्रम के लगभग एवं परमाणुओं के आकार से तुलनीय है, अत: द्रव्य की | '''एक्सरे और मणिभ संरचना''' द्रव्य की संरचना के अध्ययन में एक्सरे का विशेष स्थान है। द्रव्य के चरम रचक परमाणु हैं। परमाणुओं का आकार अत्यंत सूक्ष्म होता है, अत: उनके अध्ययन के लिए अत्यंत सूक्ष्म प्रकार के साधनों की आवश्यकता होती है। प्रकाश का तरंगदैर्घ्य परमाणुओं के आकार से बहुत अधिक होने के कारण संरचनात्मक अध्ययन में प्रकाश का विशेष उपयोग नहीं हो सकता। एक्सरे का तरंगदैर्ध्य 1 ऐंगस्ट्रम के लगभग एवं परमाणुओं के आकार से तुलनीय है, अत: द्रव्य की संरचना के अध्ययन के लिए एक्सरे उचित साधन है। द्रव्य की गैस, द्रव तथा ठोस इन तीनों अवस्थाओं के विषय में एक्सरे द्वारा अत्यंत लाभदायक ज्ञान प्राप्त हुआ है। ठोस पदार्थो की (विशेषत: मणिभों की) संरचना का यथार्थ ज्ञान सर्वप्रथम एक्सरे द्वारा ही हुआ। वर्तमान काल में एक्सरे-विश्लेषण का प्रधान उद्देश्य यह है कि ठोस अवस्था में परमाणु किस प्रकार स्थित तथा वितरित रहते हैं, यह ज्ञात किया जाए। एक अथ वा अधिक तत्वों के परमाणु जब अत्यंत निकट आते हैं तब परमाणुओं के बाह्य इलेक्ट्रानों में पारस्परिक क्रिया होती है। संतुलन होने के पश्चात् इन परमाणुओं की अंतिम रचना में स्थितिज ऊर्जा न्यूनतम होती है। अत: स्वतंत्र परमाणु और ठोस पदार्थ के बद्ध परमाणु, इन दोनों की ऊर्जाओं में भेद होता है। स्वतंत्र परमाणुओं से प्रारंभ करके उनका ठोस पदार्थो में परिवर्तन होने पर ऊर्जा का जो विनिमय होता है और अंत में ठोस पदार्थो की जो संरचनाएँ प्राप्त होती हैं, उनसे ठोस पदार्थो के गुणों की व्याख्या करना सैद्धांतिक भौतिकी का एक उद्देश्य है। वर्तमान काल में अनेक गुणों (उदाहरणार्थ विद्युच्चालकता, प्रकाशकीय स्थिरांक, स्फुरदीप्ति इत्यादि) का स्पष्टीकरण करने में अधिकांश सफलता मिल चुकी है। यह स्पष्ट है कि इस प्रकार के अध्ययन का केवल भौतिकी में ही नहीं, अपितु रसायन, टेकनॉलोजी इत्यादि विज्ञान की अन्य शाखाओं में भी अत्यंत महत्व है। ठोस पदार्थो के अनेक गुण, उनकी रासायनिक क्रियाएँ तथा स्वतंत्र परमाणुओं के गुणों के पारस्परिक संबंध का यथार्थ अध्ययन करने के लिए ठोस पदार्थो की संरचना का ज्ञान होना आवश्यक है। | ||
सामान्यत: सब ठोस पदार्थ मणिभमय होते हैं; इनमें अपवाद बहुत थोड़े हैं (उदाहरणार्थ काच, जिसे अमणिभ कहा जा सकता है)। अनेक ठोस पदार्थ (उदाहरणार्थ धातु) बाहरी रूप में मणिभ जैसे नहीं दिखाई देते हैं, तथापि एक्सरे-विश्लेषण से यह सरलता से प्रमाणित होता है कि ये सब पदार्थ भी मणिभ हैं। धातु जैसे पदार्थो के मणिभ अत्यंत सूक्ष्म होते हैं और सामान्यत: उनके क्रमबद्ध स्थापित न रहने से बाह्म रूप में धातु मणिभ जैसी नहीं दिखाई देती। उचित प्रक्रमों से धातुओं के भी इष्ट आकार के मणिभ प्राप्त हो सकते हैं। परंतु इन धात्वीय मणिभों के और उनकी सामान्य धातुओं के गुण समान नहीं रहते। अत: ठोस पदार्थो के गुण जिन मणिभ संरचनाओं पर निर्भर होते हैं, उनके अध्ययन का महत्व स्पष्ट ही है। एक्सरे द्वारा मणिभों की संरचना का अध्ययन होने के पूर्व मणिभों के बाह्म गुणों का बहुत कुछ अध्ययन हो चुका था और उनके रूपों के विषय में स्वतंत्र माणिभ ज्यामिति स्थापित हो चुकी थी। एक्सरे की सहायता में मणिभ संरचना का जो ज्ञान प्राप्त हुआ है उसका उचित बोध होने के लिए इस मणिभ ज्यामिति का परिचय आवश्यक है। | सामान्यत: सब ठोस पदार्थ मणिभमय होते हैं; इनमें अपवाद बहुत थोड़े हैं (उदाहरणार्थ काच, जिसे अमणिभ कहा जा सकता है)। अनेक ठोस पदार्थ (उदाहरणार्थ धातु) बाहरी रूप में मणिभ जैसे नहीं दिखाई देते हैं, तथापि एक्सरे-विश्लेषण से यह सरलता से प्रमाणित होता है कि ये सब पदार्थ भी मणिभ हैं। धातु जैसे पदार्थो के मणिभ अत्यंत सूक्ष्म होते हैं और सामान्यत: उनके क्रमबद्ध स्थापित न रहने से बाह्म रूप में धातु मणिभ जैसी नहीं दिखाई देती। उचित प्रक्रमों से धातुओं के भी इष्ट आकार के मणिभ प्राप्त हो सकते हैं। परंतु इन धात्वीय मणिभों के और उनकी सामान्य धातुओं के गुण समान नहीं रहते। अत: ठोस पदार्थो के गुण जिन मणिभ संरचनाओं पर निर्भर होते हैं, उनके अध्ययन का महत्व स्पष्ट ही है। एक्सरे द्वारा मणिभों की संरचना का अध्ययन होने के पूर्व मणिभों के बाह्म गुणों का बहुत कुछ अध्ययन हो चुका था और उनके रूपों के विषय में स्वतंत्र माणिभ ज्यामिति स्थापित हो चुकी थी। एक्सरे की सहायता में मणिभ संरचना का जो ज्ञान प्राप्त हुआ है उसका उचित बोध होने के लिए इस मणिभ ज्यामिति का परिचय आवश्यक है। | ||
| पंक्ति 5: | पंक्ति 5: | ||
मणिभ ज्यामिति तथा सममिति;-अ. मणिभों की विशेषता उनके बाह्य ज्यामितीय स्वरूप में है। मणिभ पृष्ठों से सीमित होते हैं और ये पृष्ठ जहाँ मिलते हैं वहाँ कोरें तथा कोने बनते हैं। इन पृष्ठों का एक दूसरे से सममित संबंध होता है। बाह्य स्वरूप के परीक्षण से यह अनुमान निकाला जा सकता है कि मणिभों में कुछ निश्चित दिशाएँ होती हैं और उनसे बाह्य स्वरूप का संबंध रहता है। इस अनुमान की सिद्धि मणिभों के अन्य गुणों से भी होती है, जैसे मणिभों की वैद्युत तथा उष्मीय चालकता, कठोरता, वर्तनांक इत्यादि गुण मणिभ के अक्ष की दिशा पर निर्भर रहते हैं। मणिभ संरचना के अध्ययन में एक्सरे का उपयोग होने के पूर्व ही यह अनुमान किया गया था कि मणिभों के उपर्युक्त गुणों का कारण उनके रचकों की क्रमबद्ध स्थापना पर आधृत हो सकता है। यदि उचित स्वरूप के रचक लिए जाएँ तो तीन आयामों में उनकी पुनरावृत्ति करके किसी भी मणिभ का स्वरूप प्राप्त हो सकता है। अत: मणिभों का स्वरूप ज्ञात करने के लिए (1) प्रधान आकार (मोटिफ़) और (2) उचित विधि से पुनरावृत्ति करने का साधन, केवल इन दो की ही आवश्यकता होती है। प्रधान आकार के स्पष्टीकरण के लिए प्राय: बिंदु लिए जाते हैं और तीन आयामों में उनकी पुनरावृत्ति के दिग्जाल (स्पेस लैटिस) बनाया जाता है। इस दिग्जाल से मणिभ की प्रतिमा (पटर्न) प्राप्त होती है। | मणिभ ज्यामिति तथा सममिति;-अ. मणिभों की विशेषता उनके बाह्य ज्यामितीय स्वरूप में है। मणिभ पृष्ठों से सीमित होते हैं और ये पृष्ठ जहाँ मिलते हैं वहाँ कोरें तथा कोने बनते हैं। इन पृष्ठों का एक दूसरे से सममित संबंध होता है। बाह्य स्वरूप के परीक्षण से यह अनुमान निकाला जा सकता है कि मणिभों में कुछ निश्चित दिशाएँ होती हैं और उनसे बाह्य स्वरूप का संबंध रहता है। इस अनुमान की सिद्धि मणिभों के अन्य गुणों से भी होती है, जैसे मणिभों की वैद्युत तथा उष्मीय चालकता, कठोरता, वर्तनांक इत्यादि गुण मणिभ के अक्ष की दिशा पर निर्भर रहते हैं। मणिभ संरचना के अध्ययन में एक्सरे का उपयोग होने के पूर्व ही यह अनुमान किया गया था कि मणिभों के उपर्युक्त गुणों का कारण उनके रचकों की क्रमबद्ध स्थापना पर आधृत हो सकता है। यदि उचित स्वरूप के रचक लिए जाएँ तो तीन आयामों में उनकी पुनरावृत्ति करके किसी भी मणिभ का स्वरूप प्राप्त हो सकता है। अत: मणिभों का स्वरूप ज्ञात करने के लिए (1) प्रधान आकार (मोटिफ़) और (2) उचित विधि से पुनरावृत्ति करने का साधन, केवल इन दो की ही आवश्यकता होती है। प्रधान आकार के स्पष्टीकरण के लिए प्राय: बिंदु लिए जाते हैं और तीन आयामों में उनकी पुनरावृत्ति के दिग्जाल (स्पेस लैटिस) बनाया जाता है। इस दिग्जाल से मणिभ की प्रतिमा (पटर्न) प्राप्त होती है। | ||
दिग्जाल की कल्पना से मणिभों की | दिग्जाल की कल्पना से मणिभों की संरचना का अध्ययन कुछ सुगम हो जाता है। चित्र 1 में एक दिग्जाल दिया है। इसमें बिंदु क्रमानुसार तीन आयामों (डाइमेन्शंस) में स्थित हैं और उनको क्रमानुसार जोड़नेवाली रेखाओं से दिग्जाल बनता है, जो आकृति में मोटी रेखाओं से दिखाई गई है। आकृति में यद्यपि एक ही प्रकार की एकक कोशिका दिखाई गई है, तथापि विचार करने पर यह स्पष्ट होगा कि ऐसी अनेक प्रकार की किंतु समान आयतन की एकक कोशिकाएँ इस दिग्जाल में बनाई जा सकती हैं। एकक कोशिका में आठ शीर्षबिंदु हैं, और प्रत्येक शीर्षबिंदु ऐसी आठ कोशिकाओं से संबंधित है। अत: माना जा सकता है कि प्रत्येक कोशिका के लिए एक ही बिंदु है। इसका अर्थ यह है कि प्रत्येक कोशिका मणिभप्रतिमा की संपूर्ण मात्रक है। इसी प्रकार से प्रत्येक मणिभ की सममिति के अनुरूप उचित कोशिकाएँ निकाली जा सकती हैं। इन एकक कोशिकाओं की कोरें (एजेज़) लघुतम लंबाइयों की होती हैं। | ||
[[चित्र:Digjal and unit cell.jpg|200px|left]] | [[चित्र:Digjal and unit cell.jpg|200px|left]] | ||
चित्र 1-दिग्जाल तथा एकक कोशिका | चित्र 1-दिग्जाल तथा एकक कोशिका | ||
| पंक्ति 142: | पंक्ति 142: | ||
परावर्तन करनेवाले तलों में से जिनका मंडलाक्ष सामान्य होता है उनसे परावर्तित किरणें एक दीर्घ वृत्त पर अभिलिखित होती हैं। प्रत्येक मंडलाक्ष उसके दीर्घवृत्त से ज्ञात किया जा सकता है। प्रत्येक बिंदु के अंक (अर्थात् जिस तल से परावर्तन होकर यह बिंदु प्राप्त हुआ है, उसके मिलर अंक) ज्ञात करने के लिए त्रिविमालेखी (स्टीरीओग्रैफ़िक) अथवा शांकव (ग्नॉमॉनिक) प्रक्षेपण का उपयोग किया जाता है। | परावर्तन करनेवाले तलों में से जिनका मंडलाक्ष सामान्य होता है उनसे परावर्तित किरणें एक दीर्घ वृत्त पर अभिलिखित होती हैं। प्रत्येक मंडलाक्ष उसके दीर्घवृत्त से ज्ञात किया जा सकता है। प्रत्येक बिंदु के अंक (अर्थात् जिस तल से परावर्तन होकर यह बिंदु प्राप्त हुआ है, उसके मिलर अंक) ज्ञात करने के लिए त्रिविमालेखी (स्टीरीओग्रैफ़िक) अथवा शांकव (ग्नॉमॉनिक) प्रक्षेपण का उपयोग किया जाता है। | ||
लावे की रीति का महत्व अधिकतर ऐतिहासिक ही है। केवल लावे की रीति से मणिभ की | लावे की रीति का महत्व अधिकतर ऐतिहासिक ही है। केवल लावे की रीति से मणिभ की संरचना का यथार्थ ज्ञान नहीं हो सकता, परंतु इस रीति से मणिभ की संरचना का अनुमान किया जा सकता है। लावे बिंदुओं की सममिति से मणिभ की सममिति की कल्पना की जा सकती है। संरचना का संपूर्ण ज्ञान होने के लिए अन्य रीतियाँ अधिक उपयुक्त होती हैं। | ||
लावे की रीति के अन्य उपयोग भी हो सकते हैं। मणिभ को यदि बल से नत किया जाए अथवा यदि मणिभ बनते समय उसमें आंतरिक विकृति हो जाए, तो लावे बिंदुओं में भी विकृतियाँ हो जाती हैं। उदाहरणार्थ, सामान्यत: मणिभ के जो लावे बिंदु आते हैं उनका दीर्घीकरण हो जाता है। यदि धातु के पतले टुकड़े को एक्सरे पार करें तो सामान्यत: लावे बिंदुओं के स्थानों पर समान तीव्रता से संकेंद्र वृत्त प्राप्त होते हैं और इन वृत्तों का केंद्र सीधे जानेवाले एक्सरे का बिंदु होता है। धातु में यदि विकृति हो तो केंद्रीय बिंदु से अरीय (त्रिजीय) रेखाएँ मिलती हैं। एक्सरे प्रतिमाओं की इन विकृतियों से धातु तथा मणिभ की आंतरिक विकृतियों का अध्ययन हो सकता है। अनेक मणिभों में (उदाहरणार्थ पेंटाएरि्थ्राटोल, सोडियम क्लोरेट, हिम इत्यादि में) लाहे बिंदुओं के अतिरिक्त निस्तेज, अतीक्ष्ण बिंदु भी आते हैं। मणिभ का ताप बढ़ाने से ये बिंदु कुछ अधिक तीक्ष्ण हो जाते हैं। सर सी.वी.रमन के अनुमान के अनुसार ये अतीक्ष्ण बिंदु (डिफ़्यूज़ स्पॉट) मणिभ के विशिष्ट कंपनों से आते हैं और ये कंपन एक्सरे की क्रिया से उत्पन्न होते हैं। किंतु लॉन्सडेल के अनुमान के अनुसार अतीक्ष्ण बिंदुओं का अस्तित्व डीबॉय-वालर के समीकरण का उपयोग करके प्रमाणित हो सकता है। | लावे की रीति के अन्य उपयोग भी हो सकते हैं। मणिभ को यदि बल से नत किया जाए अथवा यदि मणिभ बनते समय उसमें आंतरिक विकृति हो जाए, तो लावे बिंदुओं में भी विकृतियाँ हो जाती हैं। उदाहरणार्थ, सामान्यत: मणिभ के जो लावे बिंदु आते हैं उनका दीर्घीकरण हो जाता है। यदि धातु के पतले टुकड़े को एक्सरे पार करें तो सामान्यत: लावे बिंदुओं के स्थानों पर समान तीव्रता से संकेंद्र वृत्त प्राप्त होते हैं और इन वृत्तों का केंद्र सीधे जानेवाले एक्सरे का बिंदु होता है। धातु में यदि विकृति हो तो केंद्रीय बिंदु से अरीय (त्रिजीय) रेखाएँ मिलती हैं। एक्सरे प्रतिमाओं की इन विकृतियों से धातु तथा मणिभ की आंतरिक विकृतियों का अध्ययन हो सकता है। अनेक मणिभों में (उदाहरणार्थ पेंटाएरि्थ्राटोल, सोडियम क्लोरेट, हिम इत्यादि में) लाहे बिंदुओं के अतिरिक्त निस्तेज, अतीक्ष्ण बिंदु भी आते हैं। मणिभ का ताप बढ़ाने से ये बिंदु कुछ अधिक तीक्ष्ण हो जाते हैं। सर सी.वी.रमन के अनुमान के अनुसार ये अतीक्ष्ण बिंदु (डिफ़्यूज़ स्पॉट) मणिभ के विशिष्ट कंपनों से आते हैं और ये कंपन एक्सरे की क्रिया से उत्पन्न होते हैं। किंतु लॉन्सडेल के अनुमान के अनुसार अतीक्ष्ण बिंदुओं का अस्तित्व डीबॉय-वालर के समीकरण का उपयोग करके प्रमाणित हो सकता है। | ||
| पंक्ति 154: | पंक्ति 154: | ||
dhkl | dhkl | ||
इस समीकरण का तथा संरचना गुणक (स्ट्रक्चर-फ़ैक्टर)का उपयोग करके यह फल मिलता है कि (1) सरल घन में च, छ, ज (ण्, त्त्, थ्) की सब मात्राएँ संभव हैं; (2) पिंडकेंद्रित घन में च, छ, ज, (ण्, त्त्, थ्) का योगफल सम होता है; (3) फलककेंद्रित घन में च, छ, ज (ण्, त्त्, थ्) या तो सब सम होते हैं अथवा सब विषम होते हैं। यह फल चित्र 8 में दिखाया गया है। इसका उपयोग करके वर्णक्रम रेखाओं के वितरण से मणिभ की | इस समीकरण का तथा संरचना गुणक (स्ट्रक्चर-फ़ैक्टर)का उपयोग करके यह फल मिलता है कि (1) सरल घन में च, छ, ज (ण्, त्त्, थ्) की सब मात्राएँ संभव हैं; (2) पिंडकेंद्रित घन में च, छ, ज, (ण्, त्त्, थ्) का योगफल सम होता है; (3) फलककेंद्रित घन में च, छ, ज (ण्, त्त्, थ्) या तो सब सम होते हैं अथवा सब विषम होते हैं। यह फल चित्र 8 में दिखाया गया है। इसका उपयोग करके वर्णक्रम रेखाओं के वितरण से मणिभ की संरचना का अनुमान सरलता से किया जा सकता है। | ||
इसी प्रकार गणना करके टेट्रगोनल, हेक्सागोनल, इत्यादि अन्य मणिभों के लिए भी सारणियाँ बनाई गई हैं। इनका उपयोग करके प्रतिमाओं से मणिभों की संरचनाओं का अनुमान किया जा सकता है, किंतु अन्य मणिभों के लिए कार्य इतना सरल नहीं है। | इसी प्रकार गणना करके टेट्रगोनल, हेक्सागोनल, इत्यादि अन्य मणिभों के लिए भी सारणियाँ बनाई गई हैं। इनका उपयोग करके प्रतिमाओं से मणिभों की संरचनाओं का अनुमान किया जा सकता है, किंतु अन्य मणिभों के लिए कार्य इतना सरल नहीं है। | ||
| पंक्ति 186: | पंक्ति 186: | ||
वेजनबर्ग कैमरे की सफलता के पश्चात् उसमें सुधार करके अनेक कैमरे विशेष उद्देश्यों के लिए बनाए गए। इनमें सीबोल्ट-सौटर, बर्गर इत्यादि वैज्ञानिकों के कैमरे उल्लेखनीय हैं। | वेजनबर्ग कैमरे की सफलता के पश्चात् उसमें सुधार करके अनेक कैमरे विशेष उद्देश्यों के लिए बनाए गए। इनमें सीबोल्ट-सौटर, बर्गर इत्यादि वैज्ञानिकों के कैमरे उल्लेखनीय हैं। | ||
घूर्णित-मणिभ प्रतिमा से मणिभ संरचना ज्ञात करना अधिक सरल होता है। विशेषत: जिन मणिभों की | घूर्णित-मणिभ प्रतिमा से मणिभ संरचना ज्ञात करना अधिक सरल होता है। विशेषत: जिन मणिभों की संरचनाएँ सरल सममित नहीं हैं उनके लिए घूर्णित-मणिभ रीति अथवा इस रीति पर आधारित अन्य कैमरों का उपयोग अत्यावश्यक है। चित्र 9 में दी हुई प्रायोगिक रचना के अनुसार जो प्रतिमाएँ आती हैं उनका स्पष्टीकरण निम्नलिखित प्रकार से हो सकता है: | ||
(1) रश्मियों की दिशाएँ ्झ्र चित्र 11 (1) | (1) रश्मियों की दिशाएँ ्झ्र चित्र 11 (1) | ||
| पंक्ति 206: | पंक्ति 206: | ||
प्रतिष्ठित (क्लैसिकल) भौतिकी के अनुसार एक्सरे तरंगों का प्रकीर्णन इलेक्ट्रानों से होता है। प्रत्येक परमाणु में इलेक्ट्रान होते हैं और प्रत्येक इलेक्ट्रान से प्रकीर्णन होने पर एक्सरे का अंत में संपूर्ण परमाणु से प्रकीर्णन होगा। अत: विशिष्ट दिशाओं में एक्सरेओं की तीव्रता इन इलेक्ट्रानों के वितरण पर अवलंबित होगी। संपूर्ण परमाणु से प्रकीर्णन होने पर तंरग का विशिष्ट दिशा में आयाम और उसी तरंग के एक मुक्त इलेक्ट्रान से उन्हीं प्रतिबंधों के अंतर्गत प्रतिष्ठित भौतिकी के अनुसार प्राप्त आयाम, इन दोनों के अनुपात को पारमाण्वीय संरचना-गुणखंड गणना द्वारा प्राप्त किया गया है। प्रत्येक एकक-कोशिका में सामान्यत: एक से अधिक संख्या के तथा प्रकार के परमाणु होते हैं। इन सब परमाणुओं को समाविष्ट करके विशिष्ट दिशा में तरंग का जो आयाम होता है उसको मणिभ का संरचना आयाम कहते हैं। इस संरचना-आयाम से परमाणुओं के निर्देशांकों का संबंध रहता है। भिन्न भिन्न तलों के लिए गणना करके मणिभ-संरचना-गुणनखंड प्राप्त किए गए हैं। | प्रतिष्ठित (क्लैसिकल) भौतिकी के अनुसार एक्सरे तरंगों का प्रकीर्णन इलेक्ट्रानों से होता है। प्रत्येक परमाणु में इलेक्ट्रान होते हैं और प्रत्येक इलेक्ट्रान से प्रकीर्णन होने पर एक्सरे का अंत में संपूर्ण परमाणु से प्रकीर्णन होगा। अत: विशिष्ट दिशाओं में एक्सरेओं की तीव्रता इन इलेक्ट्रानों के वितरण पर अवलंबित होगी। संपूर्ण परमाणु से प्रकीर्णन होने पर तंरग का विशिष्ट दिशा में आयाम और उसी तरंग के एक मुक्त इलेक्ट्रान से उन्हीं प्रतिबंधों के अंतर्गत प्रतिष्ठित भौतिकी के अनुसार प्राप्त आयाम, इन दोनों के अनुपात को पारमाण्वीय संरचना-गुणखंड गणना द्वारा प्राप्त किया गया है। प्रत्येक एकक-कोशिका में सामान्यत: एक से अधिक संख्या के तथा प्रकार के परमाणु होते हैं। इन सब परमाणुओं को समाविष्ट करके विशिष्ट दिशा में तरंग का जो आयाम होता है उसको मणिभ का संरचना आयाम कहते हैं। इस संरचना-आयाम से परमाणुओं के निर्देशांकों का संबंध रहता है। भिन्न भिन्न तलों के लिए गणना करके मणिभ-संरचना-गुणनखंड प्राप्त किए गए हैं। | ||
एक्सरे द्वारा मणिभ | एक्सरे द्वारा मणिभ संरचना के निर्णय का मार्ग अब स्पष्ट हो गया होगा। एक्सरे व्याभंग प्रतिमा के बिंदुओं की (अथवा रेखाओं की) तीव्रताओं का मापन करके भिन्न भिन्न तलों के मणिभ-संरचना-गुणनखंड प्रयोग द्वारा पहले प्राप्त कर लिए जाते हैं। इनसे मणिभ के परमाणुओं के स्थानों का संनिकटता से अनुमान किया जा सकता है और उनके निर्देशांकों का उपयोग करके प्रमाणित समीकरणों से मणिभ-संरचना-गुणनखंड की गणना की जाती है। यदि अनुमान ठीक हो, तो इस गणना के फल में और प्रायोगिक मात्रा में विशेष भेद नहीं होता। इसके पश्चात् फूरिएविशेलषण से एकक कोशिका में इलेक्ट्रानों की घनता निकाली जाती हैं। इस विश्लेषण फल से यदि ऐसा प्रामणित हो कि अनुमानित संरचना पर्याप्त उचित नहीं थी, तो इस विश्लेषण फल द्वारा प्राप्त संरचना से पुन: विश्लेषण किया जाता है। इस प्रकार अनेक बार क्रमिक सन्निकटता से विश्लेषण करके अंत में यथार्थ मणिभ संरचना प्राप्त होती है। इस व्युत्पोदित मणिभ संरचना से मणिभ के अन्य गुणों का (उदाहरणार्थ प्रकाशीय, चुंबकीय, विद्युतीय इत्यादि गुणों का) भी स्पष्टीकरण होना आवश्यक होता है, अन्यथा अनुमानित तथा व्युत्पादित मणिभ संरचना ठीक नहीं मानी जा सकती । | ||
(6)''' उपसंहार''' –उपर्युक्त रीतियों से एक्सरे व्याभंग के विश्लेषण के पश्चात् अनेक ठोस पदार्थो की संरचनाओं का निर्णय हुआ है। अनेक ग्रंथ हैं जिनमें इस प्रकार प्राप्त ठोस पदार्थो की संरचनाएँ दी गई हैं। प्रत्येक तत्व, उनके यौगिक पदार्थ तथा कार्बधात्विक यौगिक पदार्थ इत्यादि ठोस पदार्थो की संरचनाएँ भी इन ग्रंथों में मिलेंगी। | (6)''' उपसंहार''' –उपर्युक्त रीतियों से एक्सरे व्याभंग के विश्लेषण के पश्चात् अनेक ठोस पदार्थो की संरचनाओं का निर्णय हुआ है। अनेक ग्रंथ हैं जिनमें इस प्रकार प्राप्त ठोस पदार्थो की संरचनाएँ दी गई हैं। प्रत्येक तत्व, उनके यौगिक पदार्थ तथा कार्बधात्विक यौगिक पदार्थ इत्यादि ठोस पदार्थो की संरचनाएँ भी इन ग्रंथों में मिलेंगी। | ||
| पंक्ति 212: | पंक्ति 212: | ||
मणिभ संरचना के ज्यामितीय संबंध सरल यौगिकों में स्पष्टता से दिखाई पड़ते हैं। ऐसे पदार्थो में परमाणुओं के आयन होते हैं, अत: इनको आयनीय मणिभ कहा जाता है। उदाहरणार्थ, नमक में सोडियम परमाणु का बाह्य इलेक्ट्रान दूर रहता है। और इसलिए सोडियम परमाणु धन आवेशित आयन होता है। सोडियम परमाणु का इलेक्ट्रान क्लोरीन परमाणु से संयुक्त हो जाने पर ऋण आवेशित आयन हो जाता है। धन और ऋण आयन आकर्षित होकर पास आएँगे किंतु परमाणु के अन्य इलेक्ट्रानों के तीव्र प्रतिकर्षण के कारण एक विशेष सीमा तक ही ये परमाणु आ पाएँगे और वहाँ वे संतुलित हो जाएँगे। प्रत्येक आयन विरुद्ध आवेश के आयन से परिवेष्टित रहता है। नमक में प्रत्येक सोडियम आयन 6 क्लोरीन आयनों से परिवेष्टित रहता है। किंतु क्षारीय खनिज के क्लोराइड, ब्रीमाइड तथा आयोडाइड में प्रत्येक आयन विरुद्ध आवेश के 8 आयनों से परिवेष्टित रहता है। यदि धन और ऋण आयनों की त्रिज्याओं का अनुपात कम हो (0.51), तो बड़ा 4 छोटे आयनों से परिवेष्टित होता है, उदाहरणार्थ ज़िंक ब्लेंड अथवा वूर्टसाइट।<ref>{{पुस्तक संदर्भ |पुस्तक का नाम=हिन्दी विश्वकोश, खण्ड 2|लेखक= |अनुवादक= |आलोचक= |प्रकाशक= नागरी प्रचारिणी सभा, वाराणसी|संकलन= भारत डिस्कवरी पुस्तकालय|संपादन= |पृष्ठ संख्या=216 |url=}}</ref> | मणिभ संरचना के ज्यामितीय संबंध सरल यौगिकों में स्पष्टता से दिखाई पड़ते हैं। ऐसे पदार्थो में परमाणुओं के आयन होते हैं, अत: इनको आयनीय मणिभ कहा जाता है। उदाहरणार्थ, नमक में सोडियम परमाणु का बाह्य इलेक्ट्रान दूर रहता है। और इसलिए सोडियम परमाणु धन आवेशित आयन होता है। सोडियम परमाणु का इलेक्ट्रान क्लोरीन परमाणु से संयुक्त हो जाने पर ऋण आवेशित आयन हो जाता है। धन और ऋण आयन आकर्षित होकर पास आएँगे किंतु परमाणु के अन्य इलेक्ट्रानों के तीव्र प्रतिकर्षण के कारण एक विशेष सीमा तक ही ये परमाणु आ पाएँगे और वहाँ वे संतुलित हो जाएँगे। प्रत्येक आयन विरुद्ध आवेश के आयन से परिवेष्टित रहता है। नमक में प्रत्येक सोडियम आयन 6 क्लोरीन आयनों से परिवेष्टित रहता है। किंतु क्षारीय खनिज के क्लोराइड, ब्रीमाइड तथा आयोडाइड में प्रत्येक आयन विरुद्ध आवेश के 8 आयनों से परिवेष्टित रहता है। यदि धन और ऋण आयनों की त्रिज्याओं का अनुपात कम हो (0.51), तो बड़ा 4 छोटे आयनों से परिवेष्टित होता है, उदाहरणार्थ ज़िंक ब्लेंड अथवा वूर्टसाइट।<ref>{{पुस्तक संदर्भ |पुस्तक का नाम=हिन्दी विश्वकोश, खण्ड 2|लेखक= |अनुवादक= |आलोचक= |प्रकाशक= नागरी प्रचारिणी सभा, वाराणसी|संकलन= भारत डिस्कवरी पुस्तकालय|संपादन= |पृष्ठ संख्या=216 |url=}}</ref> | ||
धातुओं की संरचना अनेक दृष्टि से महत्वपूर्ण है। सामान्यत धातुओं की | धातुओं की संरचना अनेक दृष्टि से महत्वपूर्ण है। सामान्यत धातुओं की संरचना तीन प्रकार की होती है : (1) फलककेंद्रित घन, (2) पिंडकेंद्रित घन और (3) षड्भुजीय सघन समूह (हेक्सागोनल क्लोज़पैक्ड)। एक्सरे से धातु की केवल संरचना ही नहीं अपितु अन्य गुणों का भी स्पष्टीकरण होता है; उदाहरणार्थ, उनके कणों का आकार तथा वितरण, आंतरिक विकृति, इत्यादि। धातुओं के तार खींचते समय उनके मणिभ विशेष दिशाओं में स्थापित हो जाते हैं और ऐसी परिस्थिति में एक्सरे व्याभंग से जो प्रतिमाएँ आती हैं उनको तंतुप्रतिमा (फ़ाइबर पैटर्न) कहा जाता है। इन प्रतिमाओं में वृत्तों की परिधि समान तीव्रता की नहीं होती हैं।<ref>सं.ग्रं.–सर लॉरेंस ब्रैग : द क्रिस्टलाइन स्टेट, जी. बेल ऐंड कंपनी, लंडन, 1949; एम.जे.बर्गर : एक्सरे क्रिस्टलोग्राफ़ी, जॉन वाइले ऐंड संस, न्यूयॉर्क, 1955; आर. डब्ल्यू. जेम्स : ऑप्टिकल प्रिंसिपल्स ऑव द डिफ़ैक्शन ऑव एक्सरेज़, जी. बेल ऐंड सन्स, लंडन, 1950।</ref> | ||
{{लेख प्रगति|आधार= |प्रारम्भिक=प्रारम्भिक2 |माध्यमिक= |पूर्णता= |शोध= }} | {{लेख प्रगति|आधार= |प्रारम्भिक=प्रारम्भिक2 |माध्यमिक= |पूर्णता= |शोध= }} | ||
06:39, 6 फ़रवरी 2021 के समय का अवतरण
एक्सरे और मणिभ संरचना द्रव्य की संरचना के अध्ययन में एक्सरे का विशेष स्थान है। द्रव्य के चरम रचक परमाणु हैं। परमाणुओं का आकार अत्यंत सूक्ष्म होता है, अत: उनके अध्ययन के लिए अत्यंत सूक्ष्म प्रकार के साधनों की आवश्यकता होती है। प्रकाश का तरंगदैर्घ्य परमाणुओं के आकार से बहुत अधिक होने के कारण संरचनात्मक अध्ययन में प्रकाश का विशेष उपयोग नहीं हो सकता। एक्सरे का तरंगदैर्ध्य 1 ऐंगस्ट्रम के लगभग एवं परमाणुओं के आकार से तुलनीय है, अत: द्रव्य की संरचना के अध्ययन के लिए एक्सरे उचित साधन है। द्रव्य की गैस, द्रव तथा ठोस इन तीनों अवस्थाओं के विषय में एक्सरे द्वारा अत्यंत लाभदायक ज्ञान प्राप्त हुआ है। ठोस पदार्थो की (विशेषत: मणिभों की) संरचना का यथार्थ ज्ञान सर्वप्रथम एक्सरे द्वारा ही हुआ। वर्तमान काल में एक्सरे-विश्लेषण का प्रधान उद्देश्य यह है कि ठोस अवस्था में परमाणु किस प्रकार स्थित तथा वितरित रहते हैं, यह ज्ञात किया जाए। एक अथ वा अधिक तत्वों के परमाणु जब अत्यंत निकट आते हैं तब परमाणुओं के बाह्य इलेक्ट्रानों में पारस्परिक क्रिया होती है। संतुलन होने के पश्चात् इन परमाणुओं की अंतिम रचना में स्थितिज ऊर्जा न्यूनतम होती है। अत: स्वतंत्र परमाणु और ठोस पदार्थ के बद्ध परमाणु, इन दोनों की ऊर्जाओं में भेद होता है। स्वतंत्र परमाणुओं से प्रारंभ करके उनका ठोस पदार्थो में परिवर्तन होने पर ऊर्जा का जो विनिमय होता है और अंत में ठोस पदार्थो की जो संरचनाएँ प्राप्त होती हैं, उनसे ठोस पदार्थो के गुणों की व्याख्या करना सैद्धांतिक भौतिकी का एक उद्देश्य है। वर्तमान काल में अनेक गुणों (उदाहरणार्थ विद्युच्चालकता, प्रकाशकीय स्थिरांक, स्फुरदीप्ति इत्यादि) का स्पष्टीकरण करने में अधिकांश सफलता मिल चुकी है। यह स्पष्ट है कि इस प्रकार के अध्ययन का केवल भौतिकी में ही नहीं, अपितु रसायन, टेकनॉलोजी इत्यादि विज्ञान की अन्य शाखाओं में भी अत्यंत महत्व है। ठोस पदार्थो के अनेक गुण, उनकी रासायनिक क्रियाएँ तथा स्वतंत्र परमाणुओं के गुणों के पारस्परिक संबंध का यथार्थ अध्ययन करने के लिए ठोस पदार्थो की संरचना का ज्ञान होना आवश्यक है।
सामान्यत: सब ठोस पदार्थ मणिभमय होते हैं; इनमें अपवाद बहुत थोड़े हैं (उदाहरणार्थ काच, जिसे अमणिभ कहा जा सकता है)। अनेक ठोस पदार्थ (उदाहरणार्थ धातु) बाहरी रूप में मणिभ जैसे नहीं दिखाई देते हैं, तथापि एक्सरे-विश्लेषण से यह सरलता से प्रमाणित होता है कि ये सब पदार्थ भी मणिभ हैं। धातु जैसे पदार्थो के मणिभ अत्यंत सूक्ष्म होते हैं और सामान्यत: उनके क्रमबद्ध स्थापित न रहने से बाह्म रूप में धातु मणिभ जैसी नहीं दिखाई देती। उचित प्रक्रमों से धातुओं के भी इष्ट आकार के मणिभ प्राप्त हो सकते हैं। परंतु इन धात्वीय मणिभों के और उनकी सामान्य धातुओं के गुण समान नहीं रहते। अत: ठोस पदार्थो के गुण जिन मणिभ संरचनाओं पर निर्भर होते हैं, उनके अध्ययन का महत्व स्पष्ट ही है। एक्सरे द्वारा मणिभों की संरचना का अध्ययन होने के पूर्व मणिभों के बाह्म गुणों का बहुत कुछ अध्ययन हो चुका था और उनके रूपों के विषय में स्वतंत्र माणिभ ज्यामिति स्थापित हो चुकी थी। एक्सरे की सहायता में मणिभ संरचना का जो ज्ञान प्राप्त हुआ है उसका उचित बोध होने के लिए इस मणिभ ज्यामिति का परिचय आवश्यक है।
मणिभ ज्यामिति तथा सममिति;-अ. मणिभों की विशेषता उनके बाह्य ज्यामितीय स्वरूप में है। मणिभ पृष्ठों से सीमित होते हैं और ये पृष्ठ जहाँ मिलते हैं वहाँ कोरें तथा कोने बनते हैं। इन पृष्ठों का एक दूसरे से सममित संबंध होता है। बाह्य स्वरूप के परीक्षण से यह अनुमान निकाला जा सकता है कि मणिभों में कुछ निश्चित दिशाएँ होती हैं और उनसे बाह्य स्वरूप का संबंध रहता है। इस अनुमान की सिद्धि मणिभों के अन्य गुणों से भी होती है, जैसे मणिभों की वैद्युत तथा उष्मीय चालकता, कठोरता, वर्तनांक इत्यादि गुण मणिभ के अक्ष की दिशा पर निर्भर रहते हैं। मणिभ संरचना के अध्ययन में एक्सरे का उपयोग होने के पूर्व ही यह अनुमान किया गया था कि मणिभों के उपर्युक्त गुणों का कारण उनके रचकों की क्रमबद्ध स्थापना पर आधृत हो सकता है। यदि उचित स्वरूप के रचक लिए जाएँ तो तीन आयामों में उनकी पुनरावृत्ति करके किसी भी मणिभ का स्वरूप प्राप्त हो सकता है। अत: मणिभों का स्वरूप ज्ञात करने के लिए (1) प्रधान आकार (मोटिफ़) और (2) उचित विधि से पुनरावृत्ति करने का साधन, केवल इन दो की ही आवश्यकता होती है। प्रधान आकार के स्पष्टीकरण के लिए प्राय: बिंदु लिए जाते हैं और तीन आयामों में उनकी पुनरावृत्ति के दिग्जाल (स्पेस लैटिस) बनाया जाता है। इस दिग्जाल से मणिभ की प्रतिमा (पटर्न) प्राप्त होती है।
दिग्जाल की कल्पना से मणिभों की संरचना का अध्ययन कुछ सुगम हो जाता है। चित्र 1 में एक दिग्जाल दिया है। इसमें बिंदु क्रमानुसार तीन आयामों (डाइमेन्शंस) में स्थित हैं और उनको क्रमानुसार जोड़नेवाली रेखाओं से दिग्जाल बनता है, जो आकृति में मोटी रेखाओं से दिखाई गई है। आकृति में यद्यपि एक ही प्रकार की एकक कोशिका दिखाई गई है, तथापि विचार करने पर यह स्पष्ट होगा कि ऐसी अनेक प्रकार की किंतु समान आयतन की एकक कोशिकाएँ इस दिग्जाल में बनाई जा सकती हैं। एकक कोशिका में आठ शीर्षबिंदु हैं, और प्रत्येक शीर्षबिंदु ऐसी आठ कोशिकाओं से संबंधित है। अत: माना जा सकता है कि प्रत्येक कोशिका के लिए एक ही बिंदु है। इसका अर्थ यह है कि प्रत्येक कोशिका मणिभप्रतिमा की संपूर्ण मात्रक है। इसी प्रकार से प्रत्येक मणिभ की सममिति के अनुरूप उचित कोशिकाएँ निकाली जा सकती हैं। इन एकक कोशिकाओं की कोरें (एजेज़) लघुतम लंबाइयों की होती हैं।
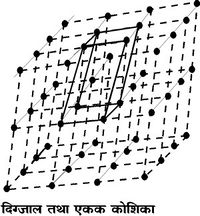
चित्र 1-दिग्जाल तथा एकक कोशिका

चित्र 2- एकक कोशिका और उसके अवयव
एकक कोशिका की तीन कोरों से तथा उनके बीच के तीन कोणों से प्रत्येक कोशिका निश्चित होती है। कोशिकाओं के इन छह अवयवों को सूचित करने की अतंरराष्ट्रीय पद्धति है, जिसमें इनके लिए ABCOabg का प्रयोग होता है। चित्र 2 में एक एकक कोशिका दिखाई गई है। इस चित्र में ABCOabg के बदले क्रमानुसार का खा गा मू आ ई ऊ का प्रयोग किया गया है। कोशिका के अवयव निम्नलिखित हैं :
लंबाई मूका = क; कोण खामूगा = आ
लंबाई मूखा = ख; कोण गामूका = ई
लंबाई मूगा = ग; कोण कामूखा = ऊ
लंबाइयों क,ख तथा ग को अक्षीय लंबाइयाँ कहते हैं और मूका, मूखा तथा मूगा इन तीन दिष्टों (वेक्टर्स) से मणिभ के अक्षों की परिभाषा होती है। 'मू' को मूल बिंदु समझकर मणिभ के किसी भी बिंदु का स्थान इकाइयों क,ख, ग में निश्चित हो सकता है। उदाहरणत: यदि मणिभ के किसी एक बिंदु के निर्दशांक य, र, ल हैं, तो हम लिख सकते हैं कि
य=प×क
र=फ×ख }}जहाँ प, फ, ब धन अथवा ऋण संख्याएँ अथवा शून्य हैं।
ल=बग×
श्
दिग्जाल तथा एकक कोशिका की कल्पना से मणिभ की अनेक विशिष्टताओं का स्पष्टीकरण करना मणिभ ज्यामिति का विकास करना सरल होता है। दिग्जाल के बिंदुओं की रचना समांतर तथा समदूरस्थ असंख्य स्तरों द्वारा स्वेच्छापूर्वक की जा सकती है। ये स्तर मणिभों के प्रमुख फलकों के समांतर होते हैं।
मणिभों के फलक निर्धारित करने के लिए पहले पूर्वोक्त स्तरों में से तीन असमांतर स्तर लिए जाते हैं। इनको हम प्रधान फलक कहेंगे। इनके प्रतिच्छेदों से मूका, मूखा, मूगा, तीन मणिभ अक्षों की दिशाएँ मिलती हैं। अब एक अन्य समतल ऐसा लिया जाता है जो तीनों प्रधान फलकों को काटता है; इस समतल को मानक समतल (स्टैंडर्ड प्लेन) कहते हैं। यह यदि का खा गा हो (चित्र 2), तो मूका, मूखा और मूगा इन अंत:खंडों की आपेक्षिक लंबाइयों से मणिभ की अक्षीय लंबाइयाँ क, ख, ग, निश्चित की जाती हैं। मणिभ का बाह्य स्वरूप निश्चित करने के लिए क, ख, ग की केवल आपेक्षिक लंबाइयों की आवश्यकता होती है; अत: सामान्यत: ख की मात्रा एक मान ली जाती है। क, ख, ग के निश्चित हो जाने पर मणिभ का कोई भी अन्य तल मणिभ अक्षों पर उसके अंत: खंडों से निश्चित होता है। मान लें ये अंत:खंड क/च, ख/छ, ग/ज हैं तो च, छ, ज इन संख्याओं को मिलर अंक कहते हैं। कोई भी फलक अथवा तल उसके मिलर अंकों द्वारा, अर्थात् च, छ, ज द्वारा सूचित किया जाता है। चित्र 2 में तल का खा गा (111) से सूचित होगा। तल मूखागा के समांतर किंतु बिंदु का में से जानेवाला तल (100) से सूचित होगा, कारण यह है कि इस तल के लिए छ=ज=µ।
जाल के किन्हीं भी दो बिंदुओं को जोड़ने पर जो सरल रेखा बनती है उसे बढ़ाने से बिंदुओं की एक पंक्ति मिलती है, जिसमें दिग्जाल के समदूरस्थ बिंदु रहते हैं। इस पंक्ति को मंडलाक्ष (ज़ोन ऐक्सिस) कहते हैं। यदि जाल के किसी एक बिंदु को, जिसके निर्देशांक (टक, टख, ढग)हैं, मूल बिंदु से जोड़ दिया जाए तो प्राप्त पंक्ति की दिशा (ट ठ ढ) एक मंडलाक्ष की दिशा होती है। यदि इस मंडलाक्ष में घनेपन से जाल बिंदु हो तो यह मंडलाक्ष महत्व के अनेक तलों के समांतर होता है।
अनेक मणिभों के फलकों के कोण नापने से यह ज्ञात हुआ कि मणिभों के बाह्य स्वरूपों में जितनी विभिन्नता दिखाई देती है उतनी वास्तव में नहीं होती और समस्त दिग्जाल केवल सात समुदायों में विभाजित किए जा सकते हैं। अन्य शब्दों में, सब मणिभों के मापित कोणों का तथा फलकों के मिलर अंकों का सात निर्देशांक पद्धतियों से स्पष्टीकरण हो सकता है। अत: मणिभों के दिग्जालों के केवल सात प्रकार हैं। चित्र 2 में एकक कोशिका की अक्षीय लंबाइयाँ तथा उनके बीच के कोण पूर्वोक्त सात पद्धतियों में भिन्न भिन्न हैं। उनकी नापें निम्नलिखित सारणी 1 में दी हुई है :
सारणी 1
सात मणिभ पद्धतियाँ और उनके लक्षण
श्
श्
दिग्जाल (चित्र 2) के बिंदुओं के आठ स्थानों के अतिरिक्त अन्य स्थान भी दिग्जाल बिंदु के लिए संभव है। ये स्थान घन मणिभों के लिए चित्र 3 में दिए गए हैं। सरल घन (चित्र 3 (1)) में आठ कोनों पर आठ बिंदु हैं। इनके अतिरिक्त घन के जो छह फलक होते हैं, उनमें प्रत्येक के ठीक मध्य पर एक एक बिंदु स्थापित करने से फलककेंद्रित घन (चित्र 3 (2)) बनता है। सरल घन के ठीक मध्य पर एक बिंदु स्थापित करने से पिंडकेंद्रित घन (चित्र 3 (3)) बनता है। इन विधियों के समावेश से तथा सारणी 1 में दी हुई सात पद्धतियों से सर्वज्ञात मणिभों के दिग्जाल तथा केवल 14 प्रकारों में विभाजित हो सकते हैं (चित्र 4 देखिए)।
श्
चित्र 3. घन मणिभ
1. सरल घन; 2. फलककेंद्रित (फ्रेस सेंटर्ड) घन;
3. पिंडकेंद्रित (बॉडी सेंटर्ड) घन।
आ. यदि मणिभ ठीक विकसित हुआ हो तो उसकी बाह्य सममिति स्पष्टता से दिखाई देती है। अध्ययन से इस सममिति के जो प्रकार स्पष्ट हुए उनको बिंदुसमुदाय (प्वाइंट ग्रूप) कहते हैं। बिंदुसमुदाय को ठीक से समझने के लिए कुछ ज्यामितीय क्रियाओं का ज्ञान आवश्यक है। मणिभों की सममिति में निम्नलिखित ज्यामितीय क्रियाओं के उदाहरण मिलते हैं:
(1) किसी एक मणिभ अक्ष के चारों ओर एक बार परिभ्रमण करने में (अर्थात् 360° घूमने में) यदि म स्थितियाँ ऐसी हों जो प्रथम स्थिति से अभिन्न हों तो मणिभ के उस अक्ष को म-बार परिभ्रमण-सममिति-अक्ष कहा जाता है। अन्य शब्दों में, 'म-बार परिभ्रमण-सममिति-अक्ष' के परित: 2p/म अंश तक घूमने से मणिभ पूर्ववत् स्थिति में आ जाता है। उदाहरणार्थ, घन मणिभ में प्रत्येक प्रमुख अक्ष 'चतुर्वार परिभ्रमण सममिति-अक्ष' होता है। प्रकृति में इस प्रकार के केवल द्वि-वार, त्रि-वार, चतुर्वार तथा षड्वार अक्ष ही होते हैं, पंच-वार तथा अन्य अक्ष नहीं होते।
(2) यदि मणिभ में एक ऐसा बिंदु अ हो कि प्रत्येक बिंदु ब तथा उसके संगत बिंदु ब´ को जोड़नेवाली सरल रेखा ब अ ब´ बिंदु अ पर समद्विभाजित होती है, तो बिंदु अ को मणिभ का सममिति केंद्र कहा जाता है। उदाहरणार्थ, घन का मध्यबिंदु सममिति केंद्र होता है। सममिति केंद्र को प्रतिलोमीकरण केंद्र भी कहते हैं।
(3) यदि मणिभ केंद्र में से होकर जाता हुआ ऐसा तल मिल सके कि मणिभ का एक अर्धभाग दूसरे अर्धभाग का (इस तल में) प्रतिबिंब हो, तो ऐसे तल को सममिति तल कहते हैं।
उपर्युक्त वर्णित क्रियाओं की मिश्र क्रियाएँ भी हो सकती हैं। यदि किसी केंद्रीय अक्ष के परित: 2p/म अंश तक परिभ्रमण के पश्चात् प्रतिलोमीकरण से पुन: पूर्ववत् मूल परिस्थिति प्राप्त होती हो, तो इस क्रिया को परिभ्रमण-प्रतिलोमीकरण कहते हैं। वैसे ही 2p/म अंश तक परिभ्रमण के पश्चात् परावर्तन से पुन: पूर्ववत् रचना प्राप्त होती हो, तो उसे परिभ्रमण-परावर्तन कहा जाता है।
परावर्तन, परिभ्रमण, प्रतिलोमीकरण, परिभ्रमण-प्रतिलोमीकरण, परिभ्रमण-परावर्तन इत्यादि प्रत्येक क्रिया को सममिति क्रिया कहते हैं। इनमें से एक अथवा अधिक क्रियाओं से मणिभों के बाह्य स्वरूपों का स्पष्टीकरण हो सकता है। क्रियाओं के इन सब प्रकारों को बिंदुसमुदाय कहते हैं। सब मणिभों के लिए (अर्थात् सारणी1में दी हुई सात पद्धतियों के लिए) केवल 32 बिंदुसमुदाय संभव हैं। इनको मणिभवर्ग कहते हैं।
क. मणिभों के बाह्य स्वरूप तथा भौतिक गुणों से उनके बिंदुसमुदायों का निगमन हो सकता है किंतु मणिभ के चरम रचक परमाणु किस प्रकार स्थित हैं तथा उसकी संरचना में किस प्रकार की सममिति है इसका यथार्थ ज्ञान नहीं हो सकता। परमाणुओं की स्थिति का ज्ञान सर्वप्रथम एक्सरे से हुआ। एकक कोशिकाओं में उपर्युक्त प्रकारों की सममितियाँ होती हैं और पूर्वोक्त क्रियाओं से कोशिकाएँ पुन: पूर्ववत् होती हैं। मणिभों में इन एकक कोशिकाओं का विस्तार तीन आयामों में होता है। जिन क्रियाओं से प्रत्यक्ष मणिभ प्राप्त होते हैं, उन्हें दिक्समुदाय कहते हैं। दिक् समुदायों के 230 प्रकार हैं।
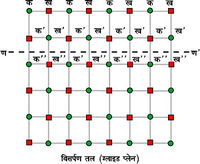
दिक्समुदायों में नवीन सममितियों का अस्तित्व संभव होता है, जो बिंदुसमुदायों में नहीं हो सकता। विसर्पण तलों (ग्लाइड प्लेन्स) का स्पष्टीकरण चित्र 5 से हो सकता है। इस आकृति में बिंदु क तथा ख क्रमानुसार वृत्त तथा वर्ग से सूचित किए गए हैं। द्वितीय पंक्ति के बिंदु´ से तथा तृतीय पंक्ति के बिंदु´´ से सूचित किए गए हैं। द्वितीय तथा तृतीय पंक्तियों के ठीक मध्य पर ण ण´ एक तल है जो कागज के तल पर अभिलंब है। इस तल ण ण´ में परावर्तन होने से द्वितीय पंक्ति के बिंदु क तृतीय पंक्ति के बिंदुओं ख के स्थानों पर चले जाएँगे। किंतु, यदि उनको परावर्तन तल के समांतर बिंदुओं (क अथवा ख) की परस्पर दूरी के अर्धभाग तक हटाया जाए, तो परिस्थिति पुन: पूर्ववत् हो जाएगी। अन्य शब्दों में, ण ण´ तल में परावर्तन के पश्चात् अर्ध-जाल-दूरी का स्थानांतरण करने से पंक्तियों पुन: प्रथम स्थिति से संपाती (कोइंसिडेंट) हो जाती, हैं। इस प्रकार के तल को (तल ण ण´को) विसर्पण तल हो जाती, हैं। इस प्रकार के तल को (ग्लाइड प्लेन) कहते हैं। तीन आयामों में जाल को संपाती करने के लिए विसर्पण तल में परावर्तन के पश्चात् प्रथम अर्ध-जाल-दूरी का स्थानांतरण विसर्पण तल के समांतर और तत्पश्चात् विसर्पण तल से लंब दिशा में अर्ध-जाल-दूरी का स्थानांतरण करना आवश्यक होगा।
यदि ण ण´ को हम अक्ष समझें, तो उसके परित: 180° के घूर्णन से बिंदु क´ बिंदु ख´´ के स्थान पर चला जायगा। अब अर्ध-जाल-दूरी का स्थानांतरण करने से प्राप्त आकृति प्रथम आकृति से संपाती होगी। इन गुणों के अक्ष को (अक्ष ण ण´) पेंच अक्ष (स्क्रू ऐक्सिस) कहते हैं। यदि बिंदुओं क (अथवा ख) का एक दूसरे से अंतर 'य' समझा जाए तो चित्र 5 में का पेंच अक्ष ण ण´ द्विवार पेच अक्ष होगा, क्योंकि यहाँ संचालन य/2 की आवयकता होती है। त्रिवार पैंच अक्ष के लिए स्थानांतरण य/3 की तथा घूर्णन 2p/3 की आवश्यकता होगी अथवा म-बारपेंच अक्ष के लिए स्थानांतरण य/म तथा घूर्णन 2p/म की आवश्यकता होगी।
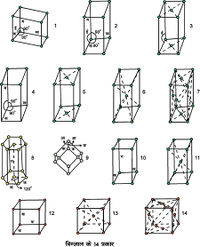
चित्र 4. दिग्जाल के 14 प्रकार
1. ट्राइक्लिनिक; 2. सरल मोनोक्लिनिक; 3. अंत्य फलककेंद्रित मोनोक्लिनिक; 4. सरल ऑर्थोरॉम्बिक; 5. अंत्य फलककेंद्रित ऑर्थोरॉम्बिक; 6. पिंडकेंद्रित ऑर्थोरॉम्बिक; .फलककेंद्रित ऑर्थोरॉम्बिक; 8. हेक्सागोनल (षड्भुजीय); 9. रॉम्बोहेड्रेल; 10. सरल टेट्रागोनल; 11. पिंडकेंद्रित टेट्रागोनल; 12. सरल घन; 13. पिंडकेंद्रित घन; 14. फलककेंद्रित घन (अक्षीय लंबाइयाँ तथा अक्षीय कोणों के लिए सारणी 1 द्र.)।
तीन आयामों में जाल सिद्धांत, जालबिंदुओं के स्थानों पर परमाणुओं की स्थापना और उपर्युक्त विसर्पण तल तथा पेंच अक्ष, इनका उपयोग करके शोनफ़्लीज ने 19वीं शताब्दी के अंत में मणिभों के वर्गीकरण में सुधार किया। जालों के 14 प्रकारों का (चित्र 4) तथा 32 बिंदुसमुदायों का उपयोग करके 230 समुदाय प्रमाणित किए गए हैं। प्रत्येक ज्ञात मणिभ इनमें के एक दिक्समुदाय के अनुसार होता है। एक्सरे-विवर्तन (व्याभंग) से मणिभों के इन ज्यामितीय सिद्धांतों का तथा दिक्समुदायों का प्रत्यक्ष प्रमाण मिलता है। अत: एक्सरे-विश्लेषण में दिक्समुदाय ज्ञात होना अत्यावश्यक होता है।
मणिभों का एक्सरे -व्याभंग-लावे, फ्ऱीडरिश और क्निपिंक ने प्रयोग द्वारा प्रथम मणिभों का एक्सरे-व्याभंग प्रस्थापित किया (द्र. एक्सरेओं की प्रकृति)। इस व्याभंग का सैद्धांतिक स्पष्टीकरण लावे ने किया। मणिभों में परमाणु क्रमबद्ध प में स्थित होते हैं। जब किसी परमाणु पर एक्सरे गिरते हैं तब उस परमाणु द्वारा (वस्तुत: उस परमाणु के इलेक्ट्रानों द्वारा) एक्सरे का प्रकीर्णन होता है। यदि परमाणुओं की पंक्ति ली जाए तो उनसे प्रकीर्णन होने पर तथा तरंगिकाओं का संयोग होने पर अंत में जो तरंगाग्र प्राप्त होगा, उसकी दिशा में व्याभंग के पश्चात् एक्सरे जाएँगे। किंतु संयोग होते समय पथ का अंतर शून्य अथवा संपूर्ण तरंगदैर्घ्य (एक अथवाअधिक) हो सकता है; अत:, प्रकाश के व्याभंग के समान, शून्य, प्रथम, द्वितीय, तृतीय इत्यादि क्रमों की एक्सरे-व्याभंजित किरणें भिन्न भिन्न दिशाओं में मिलेंगी। एक्सरे का तरंगदैर्घ्य यदि दै समझा जाए तो जिस दिशा में क्रमिक तरंगिकाओं द्वारा प्रकीरित किरणों का म× दै पथांतर होगा, उस दिशा में प्रकीर्ण किरण मिलेगी। अर्थात् यह दिशा एक शंकुतल पर होगी, क्योंकि इस शंकुतल के शीर्ष से परिधि तक गई हुई प्रत्येक रेखा के लिए उपर्युक्त प्रतिबंध संतुष्ट होगा। यह फल उचित परिवर्तन करके दो आयामोें में परमाणु-पंक्तियों के लिए भी अनुप्रयोज्य है। और आगे बढ़कर यह फल उचित परिवर्तनों के पश्चात् तीन आयामों की परमाणु-पंक्तियों के लिए (अर्थात् प्रत्यक्ष मणिभों के लिए) भी अनुप्रयोज्य होता है। गणना से यह निष्कर्ष निकलता है कि यदि जाल के परमाणुओं से व्याभंजित होकर अक्ष मू का (चित्र 2 द्र.) की परमाणु-पंक्ति से क्रम प का व्याभंग होता हो, और मू गा की परमाणु-पंक्ति से क्रम म का व्याभंग होता हो तो ज्यामिति की दृष्टि से तल प ब म से परावर्तन के तुल्य है।
यही फल ब्रैग की रीति से सरलतापूर्वक प्राप्त होता है। चित्र 6 में (1,1) मणिभ के परमाणओं की एक पंक्ति, तथा (2, 2) उसके समीप की दूसरी पंक्ति है, अर्थात् (1,1) तथा (2,2) समांतर हैं। तरंगदैर्घ्य दै का एकवर्ण एक्सरे प्रथम पंक्ति में क पर तथा द्वितीय पंक्ति में ख पर गिरता है। परविर्तनों के पश्चात् किरण 2 में पथांतर प ख फ होगा। यदि यह पथांतर न×त त हो, तो एक्सरे का परावर्तन होगा। यह प्रतिबंध निम्नलिखित समीकरण द्वारा व्यक्त हो सकता है-
2 ड ज्या था = न × त...(1)
यहाँ त = दै = तरंगदैर्घ्य
समीकरण (1) को ब्रैग का नियम कहते हैं। समीकरण (1) के सरल होने के कारण इसका अधिक उपयोग किया जाता है। यद्यपि लावे की रीति प्रकाशिकी के ज्ञात सिद्धांतों के अनुसार है तथापि ब्रैग की रीति की तुलना में वह अधिक कठिन है। यदि एक्सरे का तरंगदेर्घ्य दै ज्ञात हो तो समीकरण (1) से विशिष्ट तलपद्धति का अंतरण (स्पेसिंग) ड प्राप्त करने के लिए केवल कोण थ का मापन करना पड़ता है। आपाती एक्सरे का तरंगदैर्घ्य दै तथा जिन मणिभ तलों से परावर्तन हो रहा है उनके मिलर अंक (च, छ, ज) से जाल का अचर निकाला जा सकता है। घन, टेट्रा-
चित्र 5. विसर्पण तल (ग्लाइड प्लेन।)
गोनल तथा ऑर्थेरॉम्बिक (जिनके निर्देशाक्ष लंबकोण होते हैं) कोशिकाओं के लिए डच छ ज की मात्रा निम्नलिखत होती है :
ड2च छ ज . . (2)
घनकोशिका में क.= ख.= ग.। के अनुसार घनकोशिका के लिए
ड2च छ ज
अर्थात् समीकरण (1) के अनुसार घनकोशिका के लिए
न × तजया (थन)। . . . (3)
यहाँ थम नवें क्रम का परावर्तन कोण है। इसी प्रकार, गणना से प्रत्येक प्रकार की कोशिका के एकक अक्ष दूरी का मापन किया जा सकता है।
चित्र 6. ब्रैग का नियम; 2 ड ज्या थउ न त
यहाँ ड = मणिभ की दो समीप की परमाणु पंक्तियों का अंतर; त = आपाती एकवर्ण एक्सरे का तरंगदैर्घ्य; थ = परमाणु-पंक्ति तथा आपाती किरण के बीच का कोण (इसे ग्लैंसिंग कोण कहते हैं); न = परावर्तन का क्रमांक।
व्युत्क्रम जाल (रेसिप्रोकल लैटिस) -विवर्तन-प्रतिमा के बिंदुओं का विश्लेषण करते समय, जिन मणिभ तलों से विवर्तन होता है उनकी प्रवणताओं (स्लोप्स) का महत्व स्पष्ट होता है। प्रतिमा का प्रत्येक बिंदु विशिष्ट समांतर तलों से ब्रैग के नियमानुसार परावर्तित होकर प्राप्त होता है। इन तलों की प्रवणता तल के अभिलंब (नॉर्मल) से निश्चित होती है। अत: तल के स्थान पर अभिलंब का उपयोग करने से एक लाभ यह होता है कि तल आयामों के बदले अभिलंब के दो आयामों की ही आवश्यकता होती है, अर्थात एक आयाम कम हो जाता है। एक्सरे-विवर्तन प्रतिमा दो आयामों के फोटो-फिल्म पर ली जाती है और यह प्रतिमा एक दृष्टि से विभिन्न प्रवणताओं के तथा विभिन्न प्रकीर्णन-क्षमताओं के मणिभतलों का सरल किया हुआ प्रदर्शन है। यदि हम उपर्युक्त प्रत्येक तल के अभिलंब को इस प्रकार निश्चित करें कि इस अभिलंब की दिशा प्रवणता निश्चित करे तथा उसकी लंबाई अंतर-तल अंतरण (स्पेसिंग) डच छ ज से व्युत्क्रम हो, तो इन सब अभिलंबों के सिरे के बिंदुओं से नया बिंदुजाल प्राप्त होगा, जिसका एक्सरे-विवर्तन-प्रतिमा से साम्य होगा। इस नवीन बिंदुजाल को व्युत्क्रम जाल कहते हैं। इस प्रकार व्युत्पादित व्युत्क्रमजाल अत्यंत महत्व का होता है, क्योंकि प्रयोगों से प्राप्त एक्सरे-विवर्तन-प्रतिमा इस व्युत्क्रम-जाल का ही एक विकृत प्रतिबिंब होती है। सरल सममिति के (उदाहरणार्थ घन पद्धति के) मणिभों से जो एक्सरे-विवर्तन प्रतिमाएँ प्राप्त होती हैं, उनका विश्लेषण करके संरचना निश्चित करना विशेष कठिन नहीं होता, किंतु अन्य मणिभों के लिए संरचना का निर्णय करना अत्यंत कठिन होता है और यहाँ व्युत्क्रम जाल का उपयोग अत्यावश्यक होता है। व्युत्क्रम-जाल का उपयोग तथा विस्तार विशेषत: एवाल्ड और बर्नाल ने किया। व्युत्क्रम-जाल के उपयोग से मणिभ संरचना का निश्चय करने में विशेष सुविधा हुई और समय तथा श्रम में बहुत बचत हुई। व्युत्क्रमजाल के कुछ लक्षण और गुण नीचे दिए हुए हैं। मणिभों में दिशाओं का महत्व प्रारंभ में ही बताया गया है, अत: मणिभ संरचना की गणना में दिष्ट बीजगणित (वेक्टर ऐलजेब्रा) का उपयोग किया जाता है। व्युत्क्रम जाल की गणना में दिष्ट बीगजणित का ही उपयोग होता है। सामान्यत: दिष्ट मोटे (थिक) अक्षरों में तथा अदिष्ट साधारण अक्षरों में छापे जाते हैं।
दिष्ट जाल की एकक कोशिका क, ख, ग, (A B C) इन तीन दिष्टों से निश्चित होती है, क्योंकि यहाँ प्रत्येक दिष्ट से उसकी लंबाई तथा दिशा भी निश्चित होती है। जाल बिंदु को मूल बिंदु से जोड़नेवाला दिष्ट त्र (य, र, ल), [ R (x, y, z)] निम्नलिखित दिष्टसमीकरण के अनुसार होता है :
त्र = य क + र ख + ल ग। . . . (4)
R= xA + yB + zC . . . (4)
यहाँ य, र, ल की मात्राएँ धन अथवा ऋण पूर्ण संख्या तथा शून्य हो सकती हैं। इन दिष्टों से व्युत्क्रम जाल की परिभाषा की जाती है। व्युत्क्रम जाल तीन मूल दिष्ट क*, ख*, ग* (A* B* C*) इस प्रकार लिए जाते हैं कि दिष्ट क*(A*) दिष्ट ख (B) तथा ग (C) के अक्षों पर, दिष्ट ख* (B*) दिष्ट क (A) तथा ग (C) के अक्षों पर और दिष्ट ग* (C*) दिष्ट क (A) तथा ख (B) अक्षों पर लंब होते हैं। दिष्ट बीजगणित की भाषा में यह फल निम्नलिखित समीकरण द्वारा बताया जा सकता है:
क*.ख = क*.ग = ख*.ग = ख*.क = ग*.क = ग*.ख = 0. . . (5)
A*.B = A*.C = B*.C = B*.A = C*.A = C*.B = 0. . . (5)
यहाँ दो दिष्टों के बीच का बिंदु अदिष्ट गुणनफल का चिह्न है। व्युत्क्रमदिष्टों के परिमाण निम्नलिखित समीकरण से प्राप्त होते हैं:
क*.क = ख*.ख = ग*.ग = घ2 . . . (6)
A*.A = B*.B = C*.C = C2 . . . (6)
जहाँ घ (C) एक अचर है। सामान्यत: घ का मान एक लिया जाता है। व्युत्क्रम जाल की इस परिभाषा से उसकी एकक कोशिका तथा अन्य गुण और लक्षण (उदाहरणार्थ व्युत्क्रम अक्षों की लंबाइयाँ, कोण, आयतन इत्यादि) व्पुत्पन्न किए जा सकते हैं। व्युत्क्रम जाल का कोई भी दिष्ट त्र (च छ ज) हो, तो वह मिलर अंकों (च छ ज) के तल पर लंब होता है। दिष्ट त्र* (च छ ज) का परिमाण तल (च छ ज) के अंतरण (स्पेसिंग) ड च छ ज का व्युत्क्रम होता है। इस संक्षिप्त वर्णन से भी यह स्पष्ट होगा कि विवर्तन प्रतिमा से मणिभ संरचना का अध्ययन करने के लिए व्युत्क्रम जाल उपयुक्त साधन है। किसी भी तल के लिए ब्रैग के नियमानुसार परावर्तन होने के प्रतिबंध प्राप्त करने के लिए व्युत्क्रम जाल से परावर्तन-गोला तथा सीमा-गोला निकाले जाते हैं। इनकी सहायता से विवर्तन प्रतिमा का स्पष्टकीरण सरलता से होता है।
(1) प्रायोगिक रीतियाँ-एक्सरे द्वारा मणिभ संरचना का अध्ययन करने की प्रमुख रीतियाँ नीचे दी हुई हैं। इनका संक्षिप्त वर्णन एक्सरे की प्रकृति में मिलेगा।
(1) लावे की रीति : इस रीति में श्वेत एक्सरे का (जिसमें अनेक तरंगदैर्घ्य होते हैं) उपयोग किया जाता है। दो सूची छिद्रों में से जाने के पश्चात् एक्सरे किरणें समांतर हो जाती हैं। तब उनको मणिभ के एक छोटे से टुकड़े पर पड़ने दिया जाता है (चित्र 7)। मणिभ की इस प्रकार स्थापना की जाती है कि उसका प्रमुख अक्ष आपाती एक्सरे की दिशा से विशिष्ट कोण बनाता रहे–सामान्यत: यह कोण 00 होता है। आपाती एक्सरे के अनेक तरंगदैर्घ्यो में से उचित तरंगदैर्घ्य का ब्रैग के नियम 2ड ज्या थ = न × त के अनुसार परावर्तन होता है। परावर्तित किरणें फोटो पट्टिका पर अथवा फिल्म पर अभिलिखित होकर सामान्यत: सममित बिंदुप्रतिमा बनाती हैं। प्रतिमा के बिंदु दीर्घ वृत्ताकार वक्रों पर स्थित रहते हैं और ये बिंदु अ (अर्थात् मणिभ में से सीधे जानेवाले एक्सरे से प्राप्त बिंदु) में से जाते हैं। केवल सरल सममिति के मणिभों से सममित प्रतिमाएँ मिलती हैं, अन्यथा जटिल प्रतिमाएँ प्राप्त होती हैं। कैलसाइट मणिभ की लावे प्रतिमा नमक के मणिभ की प्रतिमा जैसी सरल और सममित नहीं है (एक्सरे की प्रकृति शीर्षक लेख से संलग्न फलक द्र., जिसमें नमक तथा कैलसाइट मणिभ की लावे प्रतिमाएँ दी हुई हैं)।
चित्र 7. लावे की रीति।
स. सूची छिद्र; म. मणिभ; प. फोटो पट्टिका
परावर्तन करनेवाले तलों में से जिनका मंडलाक्ष सामान्य होता है उनसे परावर्तित किरणें एक दीर्घ वृत्त पर अभिलिखित होती हैं। प्रत्येक मंडलाक्ष उसके दीर्घवृत्त से ज्ञात किया जा सकता है। प्रत्येक बिंदु के अंक (अर्थात् जिस तल से परावर्तन होकर यह बिंदु प्राप्त हुआ है, उसके मिलर अंक) ज्ञात करने के लिए त्रिविमालेखी (स्टीरीओग्रैफ़िक) अथवा शांकव (ग्नॉमॉनिक) प्रक्षेपण का उपयोग किया जाता है।
लावे की रीति का महत्व अधिकतर ऐतिहासिक ही है। केवल लावे की रीति से मणिभ की संरचना का यथार्थ ज्ञान नहीं हो सकता, परंतु इस रीति से मणिभ की संरचना का अनुमान किया जा सकता है। लावे बिंदुओं की सममिति से मणिभ की सममिति की कल्पना की जा सकती है। संरचना का संपूर्ण ज्ञान होने के लिए अन्य रीतियाँ अधिक उपयुक्त होती हैं।
लावे की रीति के अन्य उपयोग भी हो सकते हैं। मणिभ को यदि बल से नत किया जाए अथवा यदि मणिभ बनते समय उसमें आंतरिक विकृति हो जाए, तो लावे बिंदुओं में भी विकृतियाँ हो जाती हैं। उदाहरणार्थ, सामान्यत: मणिभ के जो लावे बिंदु आते हैं उनका दीर्घीकरण हो जाता है। यदि धातु के पतले टुकड़े को एक्सरे पार करें तो सामान्यत: लावे बिंदुओं के स्थानों पर समान तीव्रता से संकेंद्र वृत्त प्राप्त होते हैं और इन वृत्तों का केंद्र सीधे जानेवाले एक्सरे का बिंदु होता है। धातु में यदि विकृति हो तो केंद्रीय बिंदु से अरीय (त्रिजीय) रेखाएँ मिलती हैं। एक्सरे प्रतिमाओं की इन विकृतियों से धातु तथा मणिभ की आंतरिक विकृतियों का अध्ययन हो सकता है। अनेक मणिभों में (उदाहरणार्थ पेंटाएरि्थ्राटोल, सोडियम क्लोरेट, हिम इत्यादि में) लाहे बिंदुओं के अतिरिक्त निस्तेज, अतीक्ष्ण बिंदु भी आते हैं। मणिभ का ताप बढ़ाने से ये बिंदु कुछ अधिक तीक्ष्ण हो जाते हैं। सर सी.वी.रमन के अनुमान के अनुसार ये अतीक्ष्ण बिंदु (डिफ़्यूज़ स्पॉट) मणिभ के विशिष्ट कंपनों से आते हैं और ये कंपन एक्सरे की क्रिया से उत्पन्न होते हैं। किंतु लॉन्सडेल के अनुमान के अनुसार अतीक्ष्ण बिंदुओं का अस्तित्व डीबॉय-वालर के समीकरण का उपयोग करके प्रमाणित हो सकता है।
(2) चूर्ण रीति (पाउडर मेथड)–इस रीति का उपयोग यूरोप में डीबॉय तथा शिअरर ने और अमरीका में हल ने किया। यदि लावे की रीति से मणिभ के टुकड़े के स्थान पर मणिभ का महीन चूर्ण रखा जाए और एकवर्ण एक्सरे आपाती हो, तो फोटो फिल्म पर संकेंद्र वृत्त अभिलिखित होते हैं। इसका कारण सरलता से समझा जा सकता है; चूर्ण में मणिभ के तल समस्त दिशाओं में फैले रहते हैं और उनसे परावर्तित किरणोें का एक शंक्वाकार किरणपुंज निकलता है, जिसे फोटो फिल्म द्वारा काटने पर वृत्त प्राप्त होता है। यदि वृत्ताकार फिल्म का उपयोग किया जाए और वृत्त का केंद्र चूर्ण के स्थान पर हो, तो परावर्तित किरणों से वर्णक्रम के समान रेखाएँ मिलेंगी। इस रीति का उपयोग करनेे के लिए भिन्न भिन्न त्रिज्याओं के चूर्ण-कैमरे मिलते हैं। त्रिज्या जितनी अधिक होती है उतनी ही विभेदन क्षमता अधिक होती है, किंतु प्रकाशदर्शन (एक्सपोज़र) का समय भी बढ़ता जाता है। नमक तथा कैलसाइट का चूर्ण-वर्णक्रम (पाउडर स्पेक्टा) एक्सरे की प्रकृति शीर्षक लेख से संलग्न फलक में दिया हुआ है।
चूर्ण में मणिभ के तल सब दिशाओं में बिखरे हुए रहते हैं, अत: चूर्ण प्रतिमा में इन सब तलों से परावर्तन होकर वर्णक्रम मिलता है। इस रीति में वर्णक्रम की रेखाओं के मिलर अंक ज्ञात करना इतना कठिन नहीं होता। ब्रैगा के समीकरण का उपयोग करके प्रत्येक रेखा से डच छ ज (dhkl) (जाल-अंतरण) की मात्रा प्राप्त हो सकती है। इन मात्राओं से तथा वर्णक्रम-रेखाओं के वितरण से चूर्ण के मणिभ की संरचना का अनुमान किया जाता है। उदाहरणार्थ, यदि घनाकार मणिभ लिए जाएँ तो उनके तीन प्रकार हो सकते हैं (चित्र 4 द्र.)। किंतु (च छ ज) की मात्राएँ प्रत्येक के लिए निम्नलिखित भाँति की होती हैं :
डचछज
dhkl
इस समीकरण का तथा संरचना गुणक (स्ट्रक्चर-फ़ैक्टर)का उपयोग करके यह फल मिलता है कि (1) सरल घन में च, छ, ज (ण्, त्त्, थ्) की सब मात्राएँ संभव हैं; (2) पिंडकेंद्रित घन में च, छ, ज, (ण्, त्त्, थ्) का योगफल सम होता है; (3) फलककेंद्रित घन में च, छ, ज (ण्, त्त्, थ्) या तो सब सम होते हैं अथवा सब विषम होते हैं। यह फल चित्र 8 में दिखाया गया है। इसका उपयोग करके वर्णक्रम रेखाओं के वितरण से मणिभ की संरचना का अनुमान सरलता से किया जा सकता है।
इसी प्रकार गणना करके टेट्रगोनल, हेक्सागोनल, इत्यादि अन्य मणिभों के लिए भी सारणियाँ बनाई गई हैं। इनका उपयोग करके प्रतिमाओं से मणिभों की संरचनाओं का अनुमान किया जा सकता है, किंतु अन्य मणिभों के लिए कार्य इतना सरल नहीं है।
चित्र 8. घन मणिभ के विभिन्न प्रकारों के चूर्ण-वर्णक्रम रेखाओं का परस्पर संबंध
(क) सरल घन, (ख) पिंडकेंद्रित घन, (ग) फलकेंद्रित घन। सरल घन में सबसे अधिक, पिंडकेंद्रित घन में उससे कम तथा फलककेंद्रित घन में सबसे कम रेखाएँ होती हैं।
इस प्रद्धति के अन्य अनेक उपयोग होते हैं। प्रत्येक शुद्ध मणिभ की विशिष्ट चूर्ण-वर्णक्रम-रेखाएँ होती हैं और उनसे वह मणिभ पहचाना जा सकता है (जैसे पारमाण्वीय वर्णक्रमों से तत्व पहचाने जाते हैं)। अत: अज्ञात मिश्रण तथा पदार्थ का रासायनिक विश्लेषण करना चूर्ण रीति से अत्यंत सरल होता है। इसके लिए हेनावाल्ट, रिन तथा फ्रेह्वेल ने अनेक पदर्थो के लिए सारणियाँ बनाई हैं। चूर्ण वर्णक्रम की रेखाओं की स्थिति का तथा उनकी तीव्रता का मापन करके इन सारणियों से पदार्थ अथवा मिश्रणों का रासायनिक विश्लेषण शीघ्रतापूर्वक किया जाता है। यदि पदार्थ अत्यंत स्वल्प मात्रा में हो तो भी चूर्ण-रीति से उसका सूक्ष्म विश्लेषण (गाइगर-डफ्रैिक्टोमीटर) के उपयोग से चूर्ण रीति सुलभ हो गई है। इसके पहले चूर्ण रीति में जो वर्णक्रम फोटो फिल्म पर मिलता था उसके लिए 6 से लेकर 12 घंटे तक लगते थे। इसके पश्चात् फोटो फिल्म को डेवेलप करने, सुखाने इत्यादि में भी 2-3 घंटों की आवश्यकता होती थी। तत्पश्चात् वर्णक्रम रेखाओं का मापन और अंत में प्रत्येक रेखा की तीव्रता का सूक्ष्म दीप्ति-मापी (माइक्रोफोटोमीटर) से मापन इत्यादि कार्यो में बहुत समय लगता है। किंतु गाइगर व्याभंगमापी से ये सब क्रियाएँ एक साथ शीघ्रतापूर्वक होती हैं।
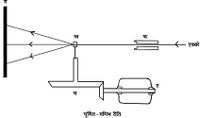
चित्र 9. घूर्णित-मणिभ रीति
क. एक्सरे समांतरित्र (कॉलीमेटर); ख मणिभ; ग. फोटो फिल्म; घ. लघुकारक योक्त्र (रिडक्शन गिअर); ङ मोटर।
(3) घूर्णित-मणिभ रीति–इस रीति का उपयोग पहले पहल सीबोल्ड और पोलान्यी ने किया। यह सबसे अधिक उपयुक्त रीति है, अत: आजकल इसी रीति पर आश्रित कई सुधारी हुई रीतियाँ प्रचलित हैं। इनमें से उचित रीति चुनकर सामान्य: किसी भी मणिभ की संरचना का विश्लेषण किया जा सकता है।
चित्र 9 में सामान्य घूर्णित-मणिभ दिखाई गई है। एकवर्ग एक्स किरर्ण समांतरित्र क में से पार होकर समांतर होती हैं और मणिभ ख एक धुरी (शैफ्ट) पर स्थित रहता है और एक विद्युत्त मोटर तथा लघुकारक योक्त्र (रिडक्शन गिअर) की सहायता से इस धुरी को मंद वेग से घुमाया जाता है। फोटो फिल्म या तो चपटी रहती है अथवा बेलनाकार फिल्म प्रयुक्त होता है; इससे परावर्तन कोण का परास बहुत बढ़ जाता है तथा विश्लेषण के लिए प्रतिमा अधिक सरल हो जाती है। मणिभ कोणमापी के शिखर पर मणिभ रखा जाता है और उसका एक प्रमुख अक्ष घूर्णन पर रखा जाता है।
इस परिस्थिति में एक प्रतिमा लेने के पश्चात् मणिभ को 90रू कोण द्वारा घुमा दिया जाता है और दूसरी प्रतिमा ली जाती है। मणिभ को पुन 90रू कोण द्वारा घुमा दिया जाता है, किंतु इस समय घुमाने का अक्ष घूर्णन अक्ष के लंबवत् होता है; अब पुन प्रतिमा ली जाती है। इस प्रकार तीन परस्पर लंबकोण अक्षों की दिशाओं में तीन प्रतिमाएँ ली जाती हैं और उनसे मणिभ के संबंध में आवश्यक ज्ञान प्राप्त किया जाता है। एक्सरे की प्रकृति शीर्षक लेख से संलग्न फलक में अभ्रक की एक घूर्णित प्रतिमा दी गई है।
कभी कभी संपूर्ण परिभ्रमण के बदले मणिभ की संरचना के अनुसार उसे विशिष्ट कोणों द्वारा घुमाकर प्रतिमा ली जाती है। यह प्रतिमा संपूर्ण परिभ्रमण से ली हुई प्रतिमा से सरल होती है। आवश्यक होने पर दोलन का कोण क्रमश: बढाकर अनेक प्रतिमाएँ ली जाती हैं। ऐसी प्रतिमाओं से विश्लेषण करना सरल होता है।
यद्यपि घूर्णित मणिभ रीति अत्यंत उपयुक्त होती है तथापि प्रतिमाओं के विश्लेषण में अनेक संशय रह जाते हैं। उनको दूर करने के लिए अनेक प्रकार के नए कैमरों का निर्माण किया गया है। इनमें वैजनबर्ग कैमरा विशेष प्रसिद्ध है। वैजनबर्ग कैमरा के प्रमुख अंग, उनका संबंध तथा कार्य चित्र 10 में दिखाए गए हैं।
वैजनबर्ग कैमरा में एकवर्ण एक्सरे मणिभ पर पूर्ववत् आपाती होते हैं और मणिभ का घूर्णनाक्ष उसके एक मुख्य अक्ष के समांतर होता है। फिल्म बेलनाकार होता है और इस बेलन का अक्ष घूर्णनाक्ष से संपाती (कोइंसिडेंट) होता है। इस कैमरे में फिल्म स्थिर नहीं रहता। उसका मंद गति से स्थानांतरण होता रहता है और यह स्थानांतरण मणिभ के घूर्णन से समक्रमिक होता है। फिल्म के स्थानांतरण की योजना से वैजनबर्ग कैमरे की विशिष्टता स्पष्ट होगी। सामान्य घूर्णित-मणिभ रीति में फिल्म स्थिर (स्टेशनरी) रहता है, इसलिए मणिभ के जिन तलों के जालअंतरण समान रहते हैं उनके लिए परावर्तन कोण समान रहता है। अत: प्रतिमा का एक बिंदु प्राप्त होता है और जब एक दूसरा समान जाल-अंतरण का तल परावर्तन के लिए उचित परिस्थिति पर पहुँचता है तब तक फिल्म का स्थानांतरण हो जाता है और समान जाल-अंतरणों के भिन्न भिन्न तलों से पृथक् बिंदु मिलते हैं।
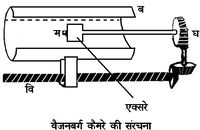
चित्र 10. वैजनबर्ग कैमरे की संरचना
म. मणिभ; ब. बेलनाकार फिल्म; घ. मणिभ के घूर्णन की योजना; वि उ फिल्म के ('घ' से समक्रमिक) विस्थापन की योजना।
वेजनबर्ग कैमरे की सफलता के पश्चात् उसमें सुधार करके अनेक कैमरे विशेष उद्देश्यों के लिए बनाए गए। इनमें सीबोल्ट-सौटर, बर्गर इत्यादि वैज्ञानिकों के कैमरे उल्लेखनीय हैं।
घूर्णित-मणिभ प्रतिमा से मणिभ संरचना ज्ञात करना अधिक सरल होता है। विशेषत: जिन मणिभों की संरचनाएँ सरल सममित नहीं हैं उनके लिए घूर्णित-मणिभ रीति अथवा इस रीति पर आधारित अन्य कैमरों का उपयोग अत्यावश्यक है। चित्र 9 में दी हुई प्रायोगिक रचना के अनुसार जो प्रतिमाएँ आती हैं उनका स्पष्टीकरण निम्नलिखित प्रकार से हो सकता है:
(1) रश्मियों की दिशाएँ ्झ्र चित्र 11 (1)
किसी महत्वपूर्ण मंडलाक्ष के घूर्णनाक्ष के समांतर रहने पर एक्सरे प्रतिमा में जो स्तररेखाएँ (लेअर लाइंस) आती हैं उनका अस्तित्व चित्र 11 से स्पष्ट हो सकता है। जब आपाती समांतर तथा एकवर्ण रेखाओं का व्याभंग परमाणुओं क तथा ख से होता है, ्झ्रचित्र 11 (1) ट तब वे किरणें जिनका पथांतर एक संपूर्ण तरंगदैर्घ्य होता है दिशा ख खव् में जाती हैं। जिनका पथांतर (ख खव्व्) दो तरंगदैर्घ्यों का होता है, वे दिशा ख खव्व् में जाती हैं। घूर्णन होते समय ऐसे अनेक तल क्रमश: इस स्थिति में आएँगे और ब्रैग के नियमानुसार उनका परार्वतन होगा। अत: जिन किरणों का पथांतर ख गव्व् है, वे दूसरे शंकु पर होंगी (चित्र 11-2) और जिनका पथांतर ख गव्व्है, तो फिल्म फैलाने पर ये सब बिंदु एक रेखा पर रहेंगे और यदि फिल्म चपटी हो (चित्र 11-3) तो प्रत्येक शंकु से प्राप्त बिंदु एक अतिपरवलय (हाइपरबोला) पर रहेंगे। यदि घूर्णन अक्ष से मणिभ का ग-अक्ष समांतर हो तो उस अक्ष से समांतर सभी तलों से क्षैतिज परावर्तन होगा और बिंदु मध्यवर्ती सरल रेखा पर प्राप्त होंगे। अर्थात् इस मध्यवर्ती रेखा पर स्थित बिंदुओं के मिलर अंक (च, छ, 0), (ण् त्त् थ्) होंगे । इस मध्यवर्ती सरल रेखा को 'शून्य स्तर' रेखा कहते हैं। इसी प्रकार स्तर रेखा के ऊपर जो बिंदु होते हैं उनके मिलर अंक (च, छ, 0), (ण् त्त् थ्) होंगे। यदि एक्सरे की दिशा तथा प्रथम स्तर रेखा के बीच का कोण फ () हो तो उसके मापन से ग (क्) की मात्रा निकाली जा सकती है, कारण
ग ज्या फ उ दै (क् च्त्द उज््ञ)
जहाँ दै (्ख्र) आपाती एकवर्ग एक्सवर्ण का तरंगदैर्घ्य है। व्युत्क्रम जाल का उपयोग करने पर इन प्रतिमाओं का विश्लेषण अधिक सरल हो जाता है। वैजनबर्ग कैमरे से जो प्रतिमाएँ आती हैं उनका रूप भिन्न होता है, किंतु उनसे निर्णय करना अधिक सुगम होता है।
श्
(2)बेलनाकार फिल्म (3) चपटी फिल्म
्झ्र चित्र 11 (2, 3) ट–घूर्णित-मणिम एक्सरे प्रतिमा की स्तररेखाओं का स्पष्टीकरण
(4) उपर्युक्त रीतियों से मणिभ की सममिति निश्चित होती है, किंतु उसकी संरचना निश्चित करने के लिए अधिक कार्य की आवश्यकता होती है। यदि केवल प्रतिमा के बिंदुओं की सममिति से मणिभ संरचना का अनुमान किया जाए, तो एक से अधिक प्रकार की संरचना संभव है, और इनमें से उचित संरचना का निर्णय करना कठिन होता है। यह समस्या हल करने के लिए प्रतिमा के बिंदुओं की (अथवा रेखाओं की) तीव्रता का मापन आवश्यक है और इस मापन के पश्चात् ही संरचना निश्चित की जा सकती है। यद्यपि दो भिन्न प्रकार के दिक्समुदाय एक ही प्रकार की सममित प्रतिमा दे सकते हैं, तथापि उनकी तीव्रताएँ भिन्न होगी। अत: किस प्रकार की संरचना से प्रतिमा में किस प्रकार तीव्रताओं का वितरण होगा, यह ज्ञात होना आवश्यक है।
प्रतिष्ठित (क्लैसिकल) भौतिकी के अनुसार एक्सरे तरंगों का प्रकीर्णन इलेक्ट्रानों से होता है। प्रत्येक परमाणु में इलेक्ट्रान होते हैं और प्रत्येक इलेक्ट्रान से प्रकीर्णन होने पर एक्सरे का अंत में संपूर्ण परमाणु से प्रकीर्णन होगा। अत: विशिष्ट दिशाओं में एक्सरेओं की तीव्रता इन इलेक्ट्रानों के वितरण पर अवलंबित होगी। संपूर्ण परमाणु से प्रकीर्णन होने पर तंरग का विशिष्ट दिशा में आयाम और उसी तरंग के एक मुक्त इलेक्ट्रान से उन्हीं प्रतिबंधों के अंतर्गत प्रतिष्ठित भौतिकी के अनुसार प्राप्त आयाम, इन दोनों के अनुपात को पारमाण्वीय संरचना-गुणखंड गणना द्वारा प्राप्त किया गया है। प्रत्येक एकक-कोशिका में सामान्यत: एक से अधिक संख्या के तथा प्रकार के परमाणु होते हैं। इन सब परमाणुओं को समाविष्ट करके विशिष्ट दिशा में तरंग का जो आयाम होता है उसको मणिभ का संरचना आयाम कहते हैं। इस संरचना-आयाम से परमाणुओं के निर्देशांकों का संबंध रहता है। भिन्न भिन्न तलों के लिए गणना करके मणिभ-संरचना-गुणनखंड प्राप्त किए गए हैं।
एक्सरे द्वारा मणिभ संरचना के निर्णय का मार्ग अब स्पष्ट हो गया होगा। एक्सरे व्याभंग प्रतिमा के बिंदुओं की (अथवा रेखाओं की) तीव्रताओं का मापन करके भिन्न भिन्न तलों के मणिभ-संरचना-गुणनखंड प्रयोग द्वारा पहले प्राप्त कर लिए जाते हैं। इनसे मणिभ के परमाणुओं के स्थानों का संनिकटता से अनुमान किया जा सकता है और उनके निर्देशांकों का उपयोग करके प्रमाणित समीकरणों से मणिभ-संरचना-गुणनखंड की गणना की जाती है। यदि अनुमान ठीक हो, तो इस गणना के फल में और प्रायोगिक मात्रा में विशेष भेद नहीं होता। इसके पश्चात् फूरिएविशेलषण से एकक कोशिका में इलेक्ट्रानों की घनता निकाली जाती हैं। इस विश्लेषण फल से यदि ऐसा प्रामणित हो कि अनुमानित संरचना पर्याप्त उचित नहीं थी, तो इस विश्लेषण फल द्वारा प्राप्त संरचना से पुन: विश्लेषण किया जाता है। इस प्रकार अनेक बार क्रमिक सन्निकटता से विश्लेषण करके अंत में यथार्थ मणिभ संरचना प्राप्त होती है। इस व्युत्पोदित मणिभ संरचना से मणिभ के अन्य गुणों का (उदाहरणार्थ प्रकाशीय, चुंबकीय, विद्युतीय इत्यादि गुणों का) भी स्पष्टीकरण होना आवश्यक होता है, अन्यथा अनुमानित तथा व्युत्पादित मणिभ संरचना ठीक नहीं मानी जा सकती ।
(6) उपसंहार –उपर्युक्त रीतियों से एक्सरे व्याभंग के विश्लेषण के पश्चात् अनेक ठोस पदार्थो की संरचनाओं का निर्णय हुआ है। अनेक ग्रंथ हैं जिनमें इस प्रकार प्राप्त ठोस पदार्थो की संरचनाएँ दी गई हैं। प्रत्येक तत्व, उनके यौगिक पदार्थ तथा कार्बधात्विक यौगिक पदार्थ इत्यादि ठोस पदार्थो की संरचनाएँ भी इन ग्रंथों में मिलेंगी।
मणिभ संरचना के ज्यामितीय संबंध सरल यौगिकों में स्पष्टता से दिखाई पड़ते हैं। ऐसे पदार्थो में परमाणुओं के आयन होते हैं, अत: इनको आयनीय मणिभ कहा जाता है। उदाहरणार्थ, नमक में सोडियम परमाणु का बाह्य इलेक्ट्रान दूर रहता है। और इसलिए सोडियम परमाणु धन आवेशित आयन होता है। सोडियम परमाणु का इलेक्ट्रान क्लोरीन परमाणु से संयुक्त हो जाने पर ऋण आवेशित आयन हो जाता है। धन और ऋण आयन आकर्षित होकर पास आएँगे किंतु परमाणु के अन्य इलेक्ट्रानों के तीव्र प्रतिकर्षण के कारण एक विशेष सीमा तक ही ये परमाणु आ पाएँगे और वहाँ वे संतुलित हो जाएँगे। प्रत्येक आयन विरुद्ध आवेश के आयन से परिवेष्टित रहता है। नमक में प्रत्येक सोडियम आयन 6 क्लोरीन आयनों से परिवेष्टित रहता है। किंतु क्षारीय खनिज के क्लोराइड, ब्रीमाइड तथा आयोडाइड में प्रत्येक आयन विरुद्ध आवेश के 8 आयनों से परिवेष्टित रहता है। यदि धन और ऋण आयनों की त्रिज्याओं का अनुपात कम हो (0.51), तो बड़ा 4 छोटे आयनों से परिवेष्टित होता है, उदाहरणार्थ ज़िंक ब्लेंड अथवा वूर्टसाइट।[1]
धातुओं की संरचना अनेक दृष्टि से महत्वपूर्ण है। सामान्यत धातुओं की संरचना तीन प्रकार की होती है : (1) फलककेंद्रित घन, (2) पिंडकेंद्रित घन और (3) षड्भुजीय सघन समूह (हेक्सागोनल क्लोज़पैक्ड)। एक्सरे से धातु की केवल संरचना ही नहीं अपितु अन्य गुणों का भी स्पष्टीकरण होता है; उदाहरणार्थ, उनके कणों का आकार तथा वितरण, आंतरिक विकृति, इत्यादि। धातुओं के तार खींचते समय उनके मणिभ विशेष दिशाओं में स्थापित हो जाते हैं और ऐसी परिस्थिति में एक्सरे व्याभंग से जो प्रतिमाएँ आती हैं उनको तंतुप्रतिमा (फ़ाइबर पैटर्न) कहा जाता है। इन प्रतिमाओं में वृत्तों की परिधि समान तीव्रता की नहीं होती हैं।[2]
|
|
|
|
|
|
टीका टिप्पणी और संदर्भ
- ↑ हिन्दी विश्वकोश, खण्ड 2 |प्रकाशक: नागरी प्रचारिणी सभा, वाराणसी |संकलन: भारत डिस्कवरी पुस्तकालय |पृष्ठ संख्या: 216 |
- ↑ सं.ग्रं.–सर लॉरेंस ब्रैग : द क्रिस्टलाइन स्टेट, जी. बेल ऐंड कंपनी, लंडन, 1949; एम.जे.बर्गर : एक्सरे क्रिस्टलोग्राफ़ी, जॉन वाइले ऐंड संस, न्यूयॉर्क, 1955; आर. डब्ल्यू. जेम्स : ऑप्टिकल प्रिंसिपल्स ऑव द डिफ़ैक्शन ऑव एक्सरेज़, जी. बेल ऐंड सन्स, लंडन, 1950।