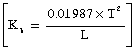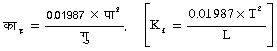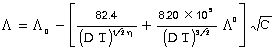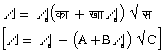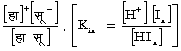भौतिक रसायन

द्रव्य की अविनाशिता के नियम के साथ ही साथ भौतिक रसायन की नींव पड़ी, यद्यपि 19वीं शती के अंत तक भौतिक रसायन को रसायन का पृथक्‌ अंग नहीं माना गया। वांट हाफ, विल्हेल्म ऑस्टवाल्ड और आरिनियस के कार्यें ने भौतिक रसायन की रूपरेखा निर्धारित की। स्थिर अनुपात और गुणित अनुपात एवं परस्पर अनुपात के नियमों ने, और बाद को आवोगाड्रो निय, गेलुसैक नियम आदि ने परमाणु और अणु की कल्पना को प्ररय दिया। परमाणुभार और अणुभार निकालने की विविध पद्धतियों का विकास किया गया। गैस संबंधी बॉयल और चार्ल्स के नियमों ने और ग्राहम के अविसरण नियमों ने इसमें सहायता दी। विलयनों की प्रकृति समझने में परासरण दाब संबंधी विचारों ने एक नवीन युग को जन्म दिया। पानी में घुलकर शक्कर के अणु उसी प्रकार अलग अलग हो जाते हैं जैसे शून्य स्थान में गैस के अणु। राउल्ट (Raoult) का वाष्पदाब संबंधी समीकरण विलयनों के संबंध में बड़े काम का सिद्ध हुआ।

(1) बॉयल-चार्ल्स समीकरण

दा´आ=झ पा [P´V=R T]

यहाँ दा (P)=दाब, आ (V)= आयतन, पा (T)=परम ताप तथा झ (R) गैस नियतांक है। यह समीकरण 1 ग्राम-अणु गैस के लिए है। यदि गैस च (n) ग्राम अणु हो, तो यह समीकरण दा´आ=च झ पा (P V= n R T) हो जाएगा।

(2) ग्राहम का समीकरण

इसमें दो गैसों के लिए क्रमश: विसरण (diffusion) की गतियाँ गा1 (D1) और गा2 (D2) हैं, गैसों के घनत्व घ1 (d1) और घ2 (d2) है, उनके अणुभार अ1 (M1) और अ2 (M2) हैं, एवं किसी छोटे से छेद में होकर गैस के निचित आयतन के विसरण का समय क्रमश: स1 (t1) और स2 (t2) है।

(3) डाल्टन का आंशिक दाब का नियम

दा=द1+द2+द3+.............

[P=p1+p2+p3+..........]

यहाँ किसी दिए हुए गैसों के मिश्रण में सब गैसों की समवेत दाब दा (P) है और उन गैसों की पृथक्‌ पृथक्‌ दाब द1 (p1), द2 (p2), द3 (p3)......आदि। ये सब गैसें आदर्श हों, इनका परम ताप पा (T) हो और सब गैसें आ (v) आयतन के पात्र में हों तो-

इसी प्रकार

.... इत्यादि

अत: गैस मिश्रण में किसी एक गैस की आंशिक दाब, द1 के लिए :

(4) परासरण दाब

इसका समीकरण भी गैस दाब के समीकरण के समान है। यदि किसी विलयन की संद्रता स (C) अणु प्रति इकाई आयतन हो और आयतन आ (V) हो (आ वह आयतन है, जिसमें विलयशील 1 अणु घुला है), तो स (C)=1/आ, (1/V)। परासरण दाब दा के लिए समीकरण यह है :

दा´आ=झ ता, दा=झ ता स [P´V=R T, P=R T C]

(5) राउल्ट (Rault) का नियम

एफ.एम. राउल्ट ने 1887 ई. में, लगभग तनु विलयन में, वाष्पदाब के सापेक्ष अवनमन के संबंध में यह नियम दिया :

इसमें विलायक की वाष्पदाब द (p), विलयन की वाष्यदाब द0 (p0), विलायक की वाष्पदाब में कमी D द (D p) और विलयन की दाब में सापेक्ष अवनमन है। विलयन में विलायक के अणुओं की संख्या च2 (n2) है, और विलेय के अणुओं की संख्या च1 (n1) है।

अगर विलयन में विलेय का द्रव्यमान द्र (w), विलेय का अणुभर भ (m) शुद्ध विलायक का द्रव्यमान द्रा (W) और विलायक का अणुभार भा (M) हो, तो

(6) विलायक में विलेय के घुलने पर विलायक की वाष्पदाब में कमी आ जाती है, और इसी कारण शुद्ध विलायक के क्वथनांक से विलयन का क्वथनांक अधिक, और शुद्ध विलायक के हिमांक से विलयन का हिमांक कम, होता है। क्वथनांक की वृद्धि D पा (D T), विलयन की सांद्रता और विलेय के अणुभार, भ (M), और विलायक के नियतांक (या क्वथनांक का आणविक उत्कर्ष), काक्व (Kb) पर निर्भर है। नीचे के समीकरण में यह का काक्व 100 ग्राम विलायक की मात्रा के लिए है।

(क ग्राम विलेय ख ग्राम विलायक में घोला गया है)

इसी प्रकार हिमांक की कमी, D पा (D T) निम्न समीकरण द्वारा व्यक्त होती है नियतांक, कह (Kf), हिमांक का आणविक अवनमन कहलाता है। 100 ग्राम विलायक के लिए यह नियतांक है।

काक्व (Kb) का संबंध विलायक के क्वथनांक पा (T) और उसके वाष्पीकरण गुप्त ऊष्मा, गु (L), से निम्नप्रकार है -

इसी प्रकार का समीकरण हिमांक के आणविक अवनमन नियतांक काह (Kf) के लिए भी है।

इसमें गु (L), हिमन की गुप्त उष्मा और पा (T) हिमांक है।

(7) द्रव्यमान समानुपाती क्रिया या द्रव्यमात्रा क्रिया का नियम

1894 ई. में गुल्डवर्ग (Guldberg) और वागे (Waage) ने इस नियम का प्रतिपादन किया। नियम यह है : 'रसायनिक अभिक्रिया का वेग अभिक्रिया में भाग लेनेवाले पदार्थों के सक्रिय द्रव्यमानों का समानुपाती होता है।' इस नियम का उपयोग बहुधा उत्क्रमणीय (reversible) क्रियाओं के साम्य के संबंध में भी किया जाता है। अभिक्रिया व्यक्त करनेवाला सर्वसामान्य समीकरण निम्नलिखित है :

क का+ख खा+ग गा+...=क¢ का¢+ख¢ खा¢+ग¢ गा¢+...

[a A+b B+c C+. . .=a¢ A¢+b¢ B¢+c¢ C¢+. . . . ]

यहाँ क्रिया में भाग लेने वाले पदार्थ का, खा, गा, (A, B, C) आदि हैं और क्रिया से उत्पन्न पदार्थ का¢, खा¢, गा¢.... (A¢, B¢, C¢) आदि हैं।

यह क्रिया उत्क्रमणीय है। साम्य स्थापित होने पर यदि का, खा, गा,.... (A, B, C....), का¢, खा¢, गा¢..... (A¢, B¢, C¢....) आदि की सांद्रताएँ क्रमश: (का), (खा), (गा),.... [(A), (B), (C),....], (का¢), (खा¢), (गा¢),.... [(A¢), (B¢), (C¢),....] आदि हों, तो सम्य नियतांक ट (K) निम्नलिखित होगा :

यह नियतांक ट (K) ताप पर र्निभर है। ऊष्मागतिकी के सिद्धांतों के अनुसार निम्न समीकरण द्वारा ट पर ताप, पा (T), का प्रभाव व्यक्त किया जाता है-

इस समीकरण में D ऊ(D u) अभिक्रिया की ऊष्मा है।

स्वतंत्र ऊर्जा, फा (F), और साम्यनियतांक, ट (K), में निम्न संबंध है, जिसे वांटहाफ का समपाती वक्र (isotherm) कहते हैं :

त फा=झ पा लघु ट - झ पा Su लघु स

d F=R T log K - R T Su log C

SC इस अभिक्रिया में भाग लेनेवाले पदार्थों की स्वयंमान्य सांद्रताएँ हैं।

(8) गिब्ज (Gibbs) का कला नियम (Phase rule)

यदि किसी निकाय (system) से संघटकों (components) की संख्या स (C) हो, और कलाओं की संख्या क (P) हो ते स्वतंत्र चर राशियों की संख्या, या स्वातंत्र की मात्रा म (F), साम्य स्थापित होने पर निम्न समीकरण द्वारा व्यक्त की जाती है :

क+म=स+2, (P+F=C+2)

अथवा म=स-क+2, (F=C-P+2)

यह गिब्ज़ का कला नियम कहलाता है। ऊष्मागतिकी संबंधी लेख में इस नियम की प्रतिपत्ति दी हुई है। इस नियम के आधार पर अनेक निकायों (जल, गंधक, मिरधातु, विलायक-मिरण) के विवरण रेखाचित्रों द्वारा व्यक्त किए जाते हैं।

(9) विद्युद्विलेषण संबंधी नियम

गाइकेल फैराडे (Faraday) ने 1883 ई. में विद्युद्विलेषण संबंधी दो नियम दिए :

(क) विद्युत्‌ धारा द्वारा उत्पन्न रासायनिक क्रिया विद्युत धारा की मात्रा की समानुपाती होती है, अर्थात्‌ जितनी धारा प्रवाहित होगी उसी के अनुपात में कोई पदार्थ निक्षिप्त या विलीन होगा।

(ख) विद्युत्‌ धारा की एक ही मात्रा द्वारा यदि कई पदार्थ निक्षिप्त, या विलीन हो रहे हों, तो उनकी मात्राएँ उसी अनुपात में होगी, जिसमें उनके रासायनिक तुल्यांक भार हैं।

इन दोनों नियमों को एक सम्मिलित समीकरण द्वारा व्यक्त किया जा सकता है। यदि किसी पदार्थ की निक्षिपत मात्रा या विलीन मात्रा व (w) ग्राम, धारा की सामर्थ्य इ (I) ऐंपियर हो, धारा के प्रवाहित होने का समय स (t) सेकंड ओर तुल्यांक भार तु (e) हो तो

समें फै (F) को फैराडे इकाई कहते हैं। फै (फैराडे) विद्युत्‌ की वह मात्रा है, जिसके प्रवाहित होने पर किसी भी पदार्थ का एक ग्राम तुल्यांक या तो निक्षिप्त होता है, या विलीन होता है :

फे=96,500 कूलंब

(10) धन और ऋण विद्युदग्रों पर धनात्मक और ऋणात्मक आयन एक ही तुल्यमात्रा में विसर्जित होते हैं, किंतु यह स्मरण रखना चाहिए कि ये आयन एक ही गति से कैथोड (cathode) या ऐनोड (anode) की ओर अग्रसर नहीं होते। यदि धनायन (cation) की गति गघ (wc) और ऋणायन (anion) की गति गअ (Ua) हो, तो धनायन की स्थानांतरण, या परिवहन (transferenc of transport) संख्या टघ (Tc) और ऋणायन की परिवहन संख्या, टअ (Ta) निम्नलिखित समीकरणों द्वारा व्यक्त की जाएगी :

हिटॉर्फ (Hittorf) ने 1853 ई. में इस परिवहन संख्याओं के निकालने की विधि निकाली।

(11) आर्रेनियस (Arrhenius) ने 1883-87 ई. में विद्युद्वियोजन की कल्पना प्रस्तुत की। जल में घुलने पर विद्युद्विलेष्य, जैसे नमक, तूतिया, अम्ल, क्षार आदि, धन और ऋण आयनों में वियोजित हो जाते हैं। यह आवयक नहीं है कि विद्युद्विलेष्यों के समस्त अणु वियोजित होते हों। ऐसीटिक अम्ल आदि के समान निर्बल विद्युद्विलेष्य कुछ प्रतिशत ही वियोजित होते हैं, किंतु सोडियम क्लोराइड, हाइड्रोक्लोरिक अम्ल, कॉस्टिक सोडा आदि के समान सबल विद्युद्विलेष्य लगभग शत प्रतिशत वियोजन, या आयनन प्रस्तुत करते हैं। आयनन की मात्रा (degree of ionisation) a (ऐल्फा) विलयन की तनुता पर निर्भर है। आर्रेनियस ने आयनन की मात्रा विलयन की विद्युच्चालकता के आधार पर निकाली। यदि किसी विलयन की विशिष्ट चालकता (specific conductivity), अर्थात्‌ विशिष्ट रोधकता (resistance) का व्युत्क्रम च (K) हो और विलयन की सांद्रता 1 ग्राम तुल्य प्रति आयतन अ (v) घन सेंमी. हो, तो उसकी तुल्य चालकता (equivalent conductivity), त, (m), निम्न समीकरण द्वारा व्यक्त की जाएगी :

त=च´अ, [m=K´v]

निर्बल विद्युत्‌ अपघट्यों की तुल्य चालकताएँ विलयन की तनुता बढ़ने पर बढ़ती जाती हैं, और जब विद्युत्‌ अपघट्यों शत प्रतिशत आयनित हो जाता है तो यह स्थिर हो जाती है। इस समय की तुल्य विद्युच्चालकता को अनंत तनुता की विद्युच्चालकता (mµ या तµ) कहते हैं। किसी तनुता, अ, पर विद्युचचालकता तअ हो और अनंत तनुता पर तµ तो आयनीकरण की मात्रा, a निम्न होगी :

अनंत तनुता पर आयनिक चालकताएँ (25° सेंटीग्रेड)

धनायन	चालकता	ऋणायन	चालकता
हा+ (H+)	349.82	औहा- (OH-)	198.5
पा+ (K+)	73.52	ब्रो- (Br-)	78.4
नाहा4+ (NH4+)	73.4	आ- (I-)	76.8
सो+ (Na+)	50.11	क्लो- (Cl-)	76.34
र+ (Ag+)	61.92	नाओ3- (NO3-)	71.44

निर्बल अम्लों के लिए ऑस्टवाल्ड (Ostwald) ने निम्नलिखित तनुता नियम (dilution law) प्रतिपादित किया- इसमें अ (u) लीटर में यह आयतन है, जिसमें विद्युत्‌ अपघट्य का एक ग्राम अणु मात्रा घुली हो। का (K), को विद्युत्‌ अपघट्य का वियोजन नियतांक (dissociation constant) कहते हैं। सबल विद्युत्‌ अपघट्य के लिए ऑस्टवाल्ड के इस समीकरण का उपयोग नहीं किया जा सकता। डेबाई (Debye) और हूकल (Huckel) ने 1923 ई. में और ऑनसैगर (Onsager) ने 1926 ई. में इन सबल विद्युत्‌ विघट्यों की विद्युच्चालकता के लिए दूसरे समीकरण दिए। पोटैशियम क्लोराइड के लिए, जिसमें दो एकसंयोजी आयन, हैं, यह समीकरण इस प्रकार है :

वि (D) विलायक का परावैद्युतांक (dielectric constant) है, ता (T) परम ताप, य (h) यानता (viscosity) और स (C) विलयन की सांद्रता (अणु प्रति लीटर, या ग्राम-तुल्यांक प्रति लीटर) है। संक्षेप में इस समीकरण को इस प्रकार लिखेंगे-

इसमें का (A) और खा (B) दिए हुए विलयाक के लिए स्थिरांक हैं, जो ताप पर ही निर्भर हैं।

(12) पानी निर्बल विद्युद्विलेष्य है :

हा2 औ = हा+ + औ हा

[H2 O = H++ O H]

पानी का आयनन नियतांक काम (Kw) = (हा+) (औ हा-) [H+] [OH-] = 80.·95 ´ 10-14 (25° सें. ताप के लिए)। पानी के इस आयनन के कारण ही जल-अपघटन होता है। जल-अपघटन का नियतांक काह (Kh) पानी के आयनन नियतांक और निर्बल अम्ल, या निर्बल क्षार के वियोजन नियतांक, पर, काआ (Ka), अम्ल के लिए एवं काक्ष (Kh) क्षार के लिए, निर्भर है।

जल-अपघटन नियतांक, का काह = जहाँ ज (h) = जल अपघटन की मात्रा, अ (v) = लीटर में वह आयतन जितने में एक ग्राम अणु यौगिक घुला हो।

काह = 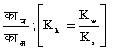(सोडियम ऐसीटेट ऐसे निर्बल अम्ल के लवण के जल-अपघटन के लिए)

काह = (अमोनियम क्लोराइड ऐसे निर्बल क्षार के लवण के लिए)।

काह = (अमोनियम ऐसीटेट ऐसे निर्बल क्षार और निर्बल अमल से बने लवण के लिए)।

(13) अम्ल और क्षारक - आयनन पर जो पदार्थ प्रोटॉन, या हाइड्रोजन आयन, हा+ (H+) देते हैं, वे अम्ल हैं और जो हाइड्रॉक्सिल आयन, औहा- (OH-) देते हैं, वे क्षारक (base) कहलाते हैं :

हाका = हा+ + का-

[ HA = H+ + A- ]

अम्ल प्रोटॉन

खा औ हा = खा+ + औहा-

[ B OH = B+ + OH- ]

ब्रान्स्टेड (Bronsted) और लाउरी (Lowry) की परिभाषा के अनुसार उस पदार्थ को अम्ल कहते हैं जिसकी प्रवृत्ति प्रोटॉन दे देने की और क्षारक वह पदार्थ है जिसकी प्रवृत्ति प्रोटॉन ले लेने की हो

का = हा+ + खा

[A = H+ + B]

अम्ल प्रोटान क्षारक

पानी में घुले हाइड्रोक्लोरिक अम्ल में निम्न साम्य है (पानी क्षारक का काम करता है)

हाक्लो + हा2औ = हा3औ + क्लो

[ HCl + H2O = H3O+ + Cl ]

अम्ल क्षारक अम्ल क्षारक

(विलयाक)

इसी प्रकार पानी (विलयाक) में घुले अमोनिया में निम्न साम्य है (पानी अम्ल का काम करता है) :

नाहा3 + हा2औ नाहा4 + औहा-

[ NH3 + H2O = NH4+ + OH-

क्षारक अम्ल अम्ल क्षारक

(विलायक)

(14) हाइड्रोजन आयन सांद्रता एवं पी-एच, (pH) क्षारक - ऐसीटिक अम्ल पानी में घुलने पर शत प्रतिशत आयनित नहीं होता। इसी प्रकार अन्य अम्ल भी पूर्ण आयनित नहीं होते। विलयन की अम्लता हाइड्रोजन आयन की सांद्रता, साहा (CH) पर निर्भर है। यह सांद्रता अनेक विधियों से निकाली जा सकती है : (क) रंग सूचकों के रंगों की तुलनना करके तथा (ख) विद्युद्वाहकबल (e. m. f.) विधि का प्रयोग करके। विलयन के हाइड्रोजन आयन की सांद्रता के अनुसार अनेक रंगसूचक रंगों का चटकीलापन प्रदर्शित करते हैं।

हाडड्रोजन आयन की सांद्रता साहा (CH) व्यक्त करने की एक सरल प्रणाली पी-एच पद्धति कहलाती है। पी-एच और साहा (CH) (सी-एच) में निम्न संबंध है :

पी-एच = - लघु साहा या (-लघु सी-एच)

[pH = -log CH,] (B) (B)

जिस विलयन का पी-एच सात से कम होता है, वह अम्लीय है, सात के निकट के पी-एच वाला विलयन शिथिल, या उदासीन है, और सात से अधिक पी-एच वाला विलयन क्षारीय है।

(15) सूचक (Indicators)

बहुत से कार्बनिक रंग ऐसे हैं, जो विलयन की विशेष पी-एच की एच सीमा में रंग में परिवर्तन प्रदर्शित करते हैं। इन उपयोग अम्ल क्षारक अनुमापनों (titration) में होता है। ये सूचक स्वयं बहुत निर्बल अम्ल,या निर्बल क्षार, हैं।

हा सू = हा+ + सू- क्षारक

[ H In = H+ + In-]

इस साम्य के लिए सूचक नियतांक का

सू =

अगले पृष्ठ की सारणी में सूचकों के ज्ञातव्य विवरण दिए गए हैं।

(16) इलेक्ट्रोड विभव (Electrode Potential) - यदि हम किसी धातु को ऐसे विलयन में डुबाएँ, जिनमें उसी धातुवाले आयन हों, तो परासरण दाब के कारण आयनों की कुछ मात्रा धातु पर जमा होना चाहेगी और विलयन दाब के अनुसार धातु का कुछ अंश विलयन में घुलना चाहेगा। इन दोनों प्रक्रियाओं में साम्य उत्पन्न हो जाने की चेष्टा रहेगी। नर्न्स्ट (Nernst) इन प्रक्रियाओं पर विचार करके एकल इलेक्ट्रोड विभव (Single Electrode Potential) की कल्पना प्रस्तुत की।

सूचक सारणी

पी-कासू = लघु कासू [pKIn = logKIn]

सूचक	पी-कास	पी-एच सीमा	रंग अम्लीय विलयन से	क्षारीय विलयन में
मेथिल वायलेट	-	0.2-3.2	पीला	बैंगनी
थायमोल ब्लू	1.7	1.2-2.8	लाल	पीला
मेथिल ऑरेंज	3.7	3.1-4.4	लाल	पीला
ब्रोमो फीनोल-ब्लू	4.0	3.0-4.6	पीला	नीला
मेथिल-रेड	5.1	4.3-6.1	लाल	पीला
लिटमस	6.5	5.5-7.5	लाल	नीला
फीनोल-रेड	7.8	6.8-8.4	पीला	लाल
फिनोल्फ़्थेलिन	9.7	8.3-10.0	रंगहीन	लाल

अगर किसी विलयन की सांद्रता, स (C) हो, अथवा सक्रियता क (a), हो, तो ताप पा (T), पर धातु इलेक्ट्रोड विभव, वि (E), निम्न समीकरण द्वारा व्यक्त किया जाएगा :

वि = वि° + स = वि° +

वि° (E°) प्रामणिक विभव है, जबकि स, या क (C or a) का मान इकाई है।

विभवों के सापेक्ष मान के लिए मानक हाइड्रोजन के इलेक्ट्रोड (Standard Hydrogen Electrode) का विभव शून्य मान लिया गया है। यह प्रत्यावर्ती हाइड्रोजन-इलेक्ट्रोड का विभव है, जब 1 वायुमंडल दाब का हाइड्रोजन एक इकाई हाइड्रोजन आयन सांद्रता के विलयन में शनै: शनै: प्रवाहित होता हो। इस इलेक्ट्रोड की अपेक्षा से अन्य इलेक्ट्रोडों का विभव, [जैसे ध+( M+) आयन के विलयन के संपर्क में धातु ध (M) का विभव] प्रदर्शित किया जाता है।

वि (E)

इस सेल का विभव वि (E) है।

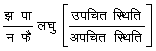
अपचयोपचय (redox) तंत्रों का विभव - यदि कोई अभिक्रिया निम्न हो-

अपचित स्थिति = उपचित स्थिति + नइ (nE)

यहाँ इ (E) = इलेक्ट्रॉनिक आवेश तथा न (n) = इलेक्ट्रान की संख्या। ऐसे तंत्रों के विभव के लिए निम्न समीकरण उपयोगी है :

वि = वि°इले -

E = E°el

पन्ने की प्रगति अवस्था

आधार

प्रारम्भिक

माध्यमिक

पूर्णता

शोध