"अंक": अवतरणों में अंतर

07:15, 14 फ़रवरी 2021 के समय का अवतरण

अंक उन चिह्नों को कहते हैं जिनसे गिनतियाँ सूचित की जाती हैं, जैसे 1, 2, 3. . .4। स्वयं गिनतियों को संख्या कहते हैं। यह निर्विवाद है कि आदिम सभ्यता में पहले वाणी का विकास हुआ और उसके बहुत काल पश्चात्‌ लेखन कला का प्रादुर्भाव हुआ। इसी प्रकार गिनना सीखने के बहुत समय बाद ही संख्याओं को अंकित करने का ढंग निकाला गया होगा। वर्तमान समय तक बचे हुए अभिलेखों में सबसे प्राचीन अंक मिस्र (ईजिप्ट) और मेसोपोटेशिया के माने जाते हैं। इनका रचनाकाल 3,000 ईसा पूर्व के आसपास रहा होगा। ये अंक चित्रलिपि (हाइरोग्लिफिक्स) के रूप में हैं। इनमें किसी अंक के लिए चिड़िया, किसी के लिए फूल, किसी के लिए कुदाल आदि बनाए जाते थे। केवल अंक ही नहीं, शब्द भी चित्रलिपि में लिखे जाते थे।

कुछ देशों में अंकों के लिए खपच्चियों पर खाँचें बनाए जाते थे, कहीं खड़िया से बिंदियाँ बनाई जाती थीं, कहीं खड़ी अथवा पड़ी लकीरों से काम लिया जाता था। प्राचीन मेसोपोटेमिया में खड़ी रेखाओं का प्रयोग होता था, जो संभवत: खड़ी अंगुलियों की द्योतक हैं:

। ।। ।।।
1 2 3

इतिहास

ब्राह्मी लिपि में, जो प्राचीन भारत में प्रचलित थी, इन्हीं संख्याओं के लिए बेंड़ी रेखाएँ प्रयुक्त होती थीं। पंडित सुधाकर द्विवेदी का विचार था कि हमारे अधिकांश नागरी अंकों की आकृतियाँ पुष्पों से ली गई हैं। परंतु शिलालेखों में से रूप कहीं भी नहीं मिले हैं। इसलिए अंकों की यह उत्पत्ति केवल कल्पना ही जान पड़ती है। आगामी पृष्ठ की सारणी में अंकों के ये रूप दिखाए गए हैं कि भारत के विविध शिलालेखों में मिलते हैं। यूनानियों में 1 से 6 तक के लिए पहले खड़ी रेखाएँ प्रयुक्त होती थीं। पीछे पांच, दस आदि गिनतियों के लिए प्रयुक्त शब्दों के प्रथम अक्षर लिखे जाने लगे। तृतीय शताब्दी ईसा पूर्व के लेखों में यह प्रणाली मिलती है। तदनंतर वर्णमाला के क्रम से लिए गए अक्षर 9 तक की क्रमागत संख्याओं के लिए प्रयुक्त होते थे, और 10, 20 आदि 90 तक, और फिर 100, 200 आदि तक के लिए शेष अक्षर प्रयुक्त होते थे।

रोमन अंक

रोमन पद्धति, जिसमें 1, 2, . . . के लिए I, II, III, IV, V, VI...लिखे जाते थे, आज तक भी थोड़ी-बहुत प्रचलित है। सन्‌ 260 ईसा पूर्व में यह पद्धति (कुछ हेरफेर के साथ) प्रचलित अवश्य थी, क्योंकि उस समय के शिलालेखों में यह वर्तमान है। रोम का साम्राज्य इतनी दूर तक फैला हुआ था और इतने समय तक शक्तिमान बना रहा कि उसकी लेखन पद्धति का प्रभुत्व आश्चर्यजनक नहीं है। अपने समय की अन्य अंक पद्धतियों से रोमन अंक पद्धति अच्छी भी थी, क्योंकि इसमें चार अक्षर V, N, L, और C तथा एक खड़ी रेखा से प्रतिदिन के व्यवहार की सभी संख्याएँ लिखी जा सकती थीं। पीछे D तथा M के उपयोग से पर्याप्त बड़ी संख्याओं का लिखना भी संभव हो गया। एक, दो और तीन के लिए इतनी ही खड़ी रेखाएँ खींची जाती थीं। V से पाँच का बोध होता था। मामसेन ने 1850 में बताया कि V वस्तुत: खुले पंजे का चित्रीय प्रतीक है और एक उलटा तथा एक सीधा V मिलाने से दो-पाँच अर्थात्‌ दस (X) बना। इस सिद्धांत से अधिकांश विद्वान् सहमत हैं। C सौ के लिए रोमन शब्द सेंडम का पहला अक्षर है और M हजार के लिए रोमन शब्द मिलि का पहला अक्षर है। बड़ी संख्या के बाईं ओर छोटी संख्या लिखकर दोनों का अंतर सूचित किया जाता था, जैसे (IV = 4)। रोमन अंकों से बहुत बड़ी संख्याएँ नहीं लिखी जा सकती थीं। आवश्यकता पड़ने पर (1) से 1,000 ((1)) से 10,000, (((1))) से 1 लाख सूचित कर लिया जाता था, परंतु जब उन्होंने 260 ईसा पूर्व में कार्षेजीव लोगों पर अपनी विजय के लिए कीर्ति स्तंभ बनाया और उस पर 23,00,000 लिखना पड़ा तो उन्हें (((1))) को 23 बार लिखना पड़ा।
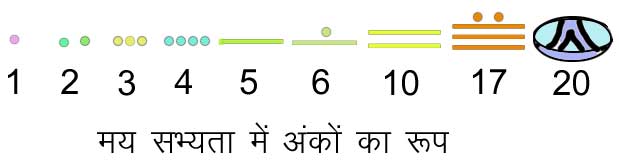
युकाटन (मेक्सिको और मध्य अमरीका के प्रायद्वीप) में प्राचीनमय सभ्यता अत्यंत विकसित अवस्था में थी। वहाँ एक, दो, तीन इत्यादि बिंदियों से 1, 2, 3, . . . सूचित किए जाते थे, बेंड़ी रेखा से 5, चक्र से 20, इत्यादि। इस प्रणाली में लिखी गई कुछ संख्याएं नीचे दिखाई गई हैं:

अंकों के लिए विशेष चिह्‌न

चीन में प्राचीन काल से ही अंकों के लिए विशेष चिह्‌न थे। यूरोप में प्रचलित अंकों 1, 2, 3,. . . की उत्पत्ति के लिए कई सिद्धांत बने, परंतु अब पाश्चात्य विद्वान् भी मानते हैं कि उनका मूल प्राचीन भारतीय पद्धति ब्राह्मी है, यद्यपि देशकाल की विभिन्नता से कई अंकों के रूप में कुछ विभिन्नता आ गई है। 2 और 3 स्पष्ट रूप से ब्राह्मी के दो और तीन, अर्थात्‌ = और 0, के घसीटकर लिखे गए रूप हैं। इसके अतिरिक्त कई अन्य यूरोपीय अंकों के रूप ब्राह्मी अंकों से मिलते हैं। उदाहरणत: 1, 4 और 6 अशोक के शिलालेखों के 1, 4 और 6 से मिलते-जुलते हैं। 2, 4, 6, 7 और नानाघाट के अंकों से बहुत कुछ मिलते हैं; 2, 3, 4, 5, 6, 7 और 9 नासिक की गुफ़ाओं के अंकों के सदृश हैं। परंतु यूरोपीय लोगों ने इन अंकों को सीधे भारतीयों से नहीं पाया। उन्होंने इन्हें अरब वालों से सीखा। इसीलिए ये अंक यूरोप में अरबी (अरेबिक) अंक कहे जाते हैं। पूर्वोक्त प्रमाणों के आधार पर वैज्ञानिक अब उन्हें हिंदू-अरेबिक अंक कहते हैं।

शून्य का प्रयोग

अशोक के शिलालेख तीसरी शताब्दी ईसा पूर्व के हैं और नानाघाट के शिलालेख लगभग 100 वर्ष बाद के हैं। इनमें हमारे अंकों के प्राचीन रूप अब भी देखे जा सकते हैं। इनमें शून्य का प्रयोग नहीं मिलता। आठवीं शताब्दी से भारत में शून्य के प्रयोग का पक्का प्रमाण मिलता है। आज संसार की अधिकांश भाषाओं में 1 से 9 तक के अंकों के लिए स्वतंत्र अंक हैं। फिर 1 में 0 लगाकर 10 बनाया जाता हैं। बाद के समस्त अंक दस को आधार मानकर बनाए जाते हैं, जैसे:

13 = 10+3
17=10+7

आधुनिक संख्या पद्धति

इसी तथ्य को हम गणित की भाषा में इस प्रकार कहते हैं कि हमारी संख्या पद्धति दशांशिक है। हम ऊपर देख चुके हैं कि गिनने की आदिम पद्धति योगात्मक थी। दो लकीरों का अर्थ दो होता था और तीन लकीरों का तीन। किंतु आधुनिक संख्या पद्धति योगात्मक भी है और गुणनात्मक भी। देखिए:

45 = 4´ 10+5
68=6´ 10+8
91=9´ 10+1

स्पष्ट है कि 45 में 4 का संख्यात्मक मान तो 4 ही है, किंतु अपनी स्थिति के कारण उसका मान 40 है। इस प्रकार 40 में 5 जोड़ने से 45 प्राप्त होता है। स्थानों के मान इकाई, दहाई, सैकड़ा आदि प्रसिद्ध हैं। जब किसी स्थान में कोई अंक नहीं रहता तब वहाँ शून्य (0) लिख दिया जाता है। जब तक शून्य का आविष्कार नहीं हुआ था तब तक स्थानिक मानों का प्रयोग भली-भाँति नहीं हो पाता था। शून्य का आविष्कार प्राचीन भारतीयों ने ही किया था। शून्यरहित प्रणालियों में (जैसे रोमन पद्धति में) बड़ी संख्याओं का लिखना बहुत कठिन होता है, और बड़ी संख्याओं को बड़ी संख्याओं से गुणा करना तो प्राय: असंभव हो जाता है।^[1]

पन्ने की प्रगति अवस्था

आधार

प्रारम्भिक

माध्यमिक

पूर्णता

शोध

टीका टिप्पणी और संदर्भ

↑ अंक (हिंदी) भारतखोज। अभिगमन तिथि: 28 जनवरी, 2014।

@@ पंक्ति 28: / पंक्ति 28: @@
 </poem>
 स्पष्ट है कि 45 में 4 का संख्यात्मक मान तो 4 ही है, किंतु अपनी स्थिति के कारण उसका मान 40 है। इस प्रकार 40 में 5 जोड़ने से 45 प्राप्त होता है। स्थानों के मान इकाई, दहाई, सैकड़ा आदि प्रसिद्ध हैं। जब किसी स्थान में कोई अंक नहीं रहता तब वहाँ शून्य (0) लिख दिया जाता है। जब तक शून्य का आविष्कार नहीं हुआ था तब तक स्थानिक मानों का प्रयोग भली-भाँति नहीं हो पाता था। शून्य का आविष्कार प्राचीन भारतीयों ने ही किया था। शून्यरहित प्रणालियों में (जैसे रोमन पद्धति में) बड़ी संख्याओं का लिखना बहुत कठिन होता है, और बड़ी संख्याओं को बड़ी संख्याओं से गुणा करना तो प्राय: असंभव हो जाता है।<ref>{{cite web |url=http://bharatkhoj.org/india/%E0%A4%85%E0%A4%82%E0%A4%95 |title=अंक|accessmonthday=28 जनवरी |accessyear=2014 |last= |first= |authorlink= |format= |publisher=भारतखोज |language= हिंदी}}</ref>
 {{लेख प्रगति|आधार=|प्रारम्भिक=प्रारम्भिक3 |माध्यमिक= |पूर्णता= |शोध= }}
 ==टीका टिप्पणी और संदर्भ==
 <references/>
 ==संबंधित लेख==
-[[Category: गणित]]
+{{गणित}}
-[[Category: हिन्दी विश्वकोश]][[Category: विज्ञान कोश]]
+[[Category:गणित]][[Category:अंकगणित]][[Category:संख्या]][[Category: हिन्दी विश्वकोश]][[Category:विज्ञान कोश]]
 __INDEX__
 __NOTOC__