आपेक्षिकता सिद्धांत

आपेक्षिकता सिद्धांत (रिलेटिविटी थ्योरी) संक्षेप में यह है कि 'निरपेक्ष' गति तथा 'निरपेक्ष' त्वरण का अस्तित्व असंभव है, अर्थात्‌ 'निरपेक्ष गति' एवं 'निरपेक्ष त्वरण' शब्द वस्तुत: निरर्थक हैं। यदि 'निरपेक्ष गति' का अर्थ होता तो वह अन्य पिंडो की चर्चा किए बिना ही निश्चित हो सकती। परंतु सब प्रकार से चेष्टा करने पर भी किसी पिंड की 'निरपेक्ष' गति का पता निश्चित रूप से प्रयोग द्वारा प्रमाणित नहीं हो सका है और अब तो आपेक्षिकता सिद्धांत बताता है कि ऐसा निश्चित करना असंभव है। आपेक्षिकता सिद्धांत से भौतिकी में एक नए दृष्टिकोण का प्रारंभ हुआ। भौतिकी के कतिपय पुराने सिद्धांतों का दृढ़ स्थान आपेक्षिकता सिद्धांत से डिग गया और अनेक मौलिक कल्पनाओं के विषय में सूक्ष्म विचार करने की आवश्यकता दिखाई देने लगी। विज्ञान में सिद्धांत का कार्य प्राय: ज्ञात फलों को व्यवस्थित रूप से सूत्रित करना होता है और तत्पश्चात्‌ उस सिद्धांत से नए फलों का अनुमान करके प्रयोग द्वारा उन फलों की परीक्षा की जाती है। आपेक्षिकता सिद्धांत इन दोनों कायाँ में सफल रहा है।

19 वीं शताब्दी के अंत तक भौतिकी का विकास न्यूटन प्रणीत सिद्धांतों के अनुसार हो रहा था। प्रत्येक नए आविष्कार अथवा प्रायोगिक फल को इन सिद्धांतों के दृष्टिकोण से देखा जाता था और आवश्यक नई परिकल्पनाएँ बनाई जाती थीं। इनमें सर्वव्यापी ईथर का एक विशिष्ट स्थान था। ईथर के अस्तित्व की कल्पना करने के दो प्रमुख कारण थे। प्रथम तो विद्युच्चुंबकीय तरंगों के कंपन का एक स्थान से दूसरे स्थान तक प्रसरण होने के लिए ईथर जैसे माध्यम की आवश्यकता थी। द्वितीय, याँत्रिकी में न्यूटन के गति तथा त्वरण विषयक समीकरणों के लिए, और जिस पार्श्वभूमि पर ये समीकरण आधारित थे उसके लिए भी, एक प्रामाणिक निर्देशक (स्टैंडर्ड ऑव रेफ़रेंस) की आवश्यकता थी। प्रयोगों के फलों का यथार्थ आकलन होने के लिए ईथर पर विशिष्ट गुणधर्मो का आरोपण किया जाता था। ईथर सर्वव्यापी समझा जाता था और संपूर्ण दिशाओं में तथा पिंडों में भी उसका अस्तित्व माना जाता था। इस स्थिर ईथर में पिंड बिना प्रतिरोध के भ्रमण कर सकते हैं, ऐसी कल्पना थी। इन गुणों के कारण ईथर को निरपेक्ष मानक समझने में कोई बाधा नहीं थी। प्रकाश की गति 3´1010 सें. मी. प्रति सेकेंड है, यह ज्ञात हुआ था और प्रकाश की तरंगें 'स्थिर' ईथर के सापेक्ष इस गति से विकीरित होती हैं, ऐसी कल्पना थी। याँत्रिकी में गति, त्वरण, बल इत्यादि के लिए भी ईथर निरपेक्ष मानक समझा जाता था।

19वीं शताब्दी के उत्तरार्ध में ईथर का अस्तित्व तथा उसके गुणधर्म स्थापित करने के अनेक प्रयत्न प्रयोग द्वारा किए गए। इनमें माइकेलसनमॉर्ले का प्रयोग विशेष महत्वपूर्ण तथा उल्लेखनीय है। (द्र. माइकेलसनमॉर्ले का प्रयोग)। पृथ्वी सूर्य की परिक्रमा ईथर के सापेक्ष जिस गति से करती है उस गति का यथार्थ मापन करना इस प्रयोग का उद्देश्य था। किंतु यह प्रयत्न असफल रहा और प्रयोग के फल से यह अनुमान निकाला गया कि ईथर के सापेक्ष पृथ्वी की गति शून्य है। इसका यह भी अर्थ हुआ कि ईथर की कल्पना असत्य है, अर्थात्‌ ईथर का अस्तित्व ही नहीं है। यदि ईथर ही नहीं है तो निरपेक्ष मानक का भी अस्तित्व नहीं हो सकता। अत: गति केवल सापेक्ष ही हो सकती है। भौतिकी में सामान्यत: गति का मापन करने के लिए अथवा फल व्यक्त करने के लिए किसी भी एक पद्धति का निर्देश (रेफ़रेंस) देकर कार्य किया जाता है। किंतु इन निर्देशक पद्धतियों में कोई भी पद्धति 'विशिष्टतापूर्ण' नहीं हो सकती, क्योंकि यदि ऐसा होता तो उस 'विशिष्टतापूर्ण' निर्देशक पद्धति को हम विश्रांति का मानक समझ सकते। अनेक प्रयोगों से ऐसा ही फल प्राप्त हुआ।

इन प्रयोगों के फलों से केवल भौतिकी में ही नहीं, प्रत्युत विज्ञान तथा दर्शन में भी गंभीर अशांति उत्पन्न हुई। 20वीं शताब्दी के प्रारंभ में (1904 में) प्रसिद्ध फ़ेच गणितज्ञ एच. पॉइन्कारे ने आपेक्षिकता का प्रनियम प्रस्तुत किया । इनके अनुसार भौतिकी के नियम ऐसे स्वरूप में व्यक्त होने चाहिए कि वे किसी भी प्रेक्षक (देखनेवाले) के लिए वास्तविक हों। इसका अर्थ यह है कि भौतिकी के नियम प्रेक्षक की गति के ऊपर अवलंबित न रहें। इस प्रनियम से दिक्‌ तथा काल की प्रचलित धारणाओं पर नया प्रकाश पड़ा। इस विषय में आइंस्टाइन की विचारधारा, यद्यपि वह कांतिकारक थी, प्रयोगों के फलों को समझाने में अधिक सफल रही। आइंस्टाइन ने गति, त्वरण, दिक्‌, काल इत्यादि मौलिक शब्दों का और उनसे संयुक्त प्रचलित धारणाओं का विशेष विश्लेषण किया। इस विश्लेषण से यह स्पष्ट हुआ कि न्यूटन के सिद्धांतों पर आधारित तथा प्रतिष्ठित भौतिकी में त्रुटियाँ हैं। आइंस्टीन प्रणीत आपेक्षिकता सिद्धांत के दो विभाग हैं : (1) विशिष्ट आपेक्षिकता सिद्धांत और (2) व्यापक आपेक्षिकता सिद्धांत। विशिष्ट आपेक्षिकता सिद्धांत में भौतिकी के नियम इस स्वरूप में व्यक्त होते हैं कि वे किसी भी अत्वरित प्रेक्षक के लिए समान होंगे। व्यापक आपेक्षिकता सिद्धांत में भौतिकी के नियम इस प्रकार व्यक्त होते हैं कि वे प्रेक्षक की गति से स्वतंत्र या अबाधित होंगे। विशिष्ट आपेक्षिकता सिद्धांत का विकास 1905 में हुआ और व्यापक आपेक्षिकता सिद्धांत का विकास 1915 में हुआ।

विशिष्ट आपेक्षिकता सिद्धांत-विशिष्ट आपेक्षिकता सिद्धांत समझना सरल होने के कारण उसपर विचार पहले किया जायगा। नित्य व्यवहार में किसी नए पदार्थ का स्थान निश्चित करने के लिए हम ज्ञात पदार्थों का निर्देश करते हैं और उनके सापेक्ष नए पदार्थ का स्थान सूचित करते हैं। इसी प्रकार गति का निश्चय होता है, किंतु गति के निश्चय के लिए उसकी दिशा तथा वेग ज्ञात करने की आवश्यकता होती है। रेलगाड़ी या विमान का वेग पृथ्वी को स्थिर समझकर निश्चित किय जाता है। किंतु पृथ्वी स्थिर नहीं है, वह अपने अक्ष पर घूमती रहती है और साथ ही सूर्य का परिभ्रमण करती रहती है। सूर्य भी स्थिर नहीं है, अन्य तारों के सापेक्ष वह अपनी ग्रहसंस्था के साथ विशिष्ट वेग से भ्रमण कर रहा हैं। विमान, पृथ्वी, सूर्य इत्यादि पदार्थों की गति स्पष्ट करने के लिए हमने जिस पदार्थ की स्वेच्छा से 'स्थिर' समझा है वह हो सकता है, अन्य निर्देशकों के सापेक्ष 'स्थिर' हो या न हो। क्षण मात्र के लिए यदि हम कल्पना करें कि आकाश में केवल एक ही पिंड है और कहीं भी कोई अन्य पदार्थ नहीं है, तो ऐसे पदार्थ के लिए 'विश्रांति' तथा 'गति' की धारणा निरर्थक है। अत: गति अथवा विश्रांति की धारणाएँ केवल सापेक्ष ही हो सकती हैं। इसी प्रकार विमान या रेलगाड़ी की 'निरपेक्ष गति' निकालना असंभव है। विशिष्ट आपेक्षिकता सिद्धांत एक अन्य रूप में भी व्यक्त किया गया है: प्रकाश की गति सब प्रेक्षकों के लिए (वस्तुत: केवल ऐसे प्रेक्षकों के लिए जिनके ऊपर कोई भी बल कार्य न कर रहा हो) अचर है, अर्थात्‌ उतनी ही रहती है, बदलती नहीं।

विशिष्ट आपेक्षिकता सिद्धांत इस प्रकार सरल ही दिखाई देता है, परतु भौतिकी के भिन्न-भिन्न क्षेत्रों में इसका उपयोग करने के पश्चात्‌ जो फल प्राप्त होते हैं, वे नित्य व्यवहार के फलों की तुलना में अत्यंत आश्चर्यजनक हैं। नित्य व्यवहार में जो वर्ग हमारे सामने आते हैं, वे प्रकाश के वेग की तुलना में उपेक्षणीय होते हैं और ऐसे वेगों के लिए न्यूटन के (अर्थात प्रतिष्ठित भौतिकी के) सिद्धांत तथा नियम उपयुक्त हैं। जब प्रकाश के वेग के समीप के वेगों का प्रश्न आता है, तभी न्यूटन के नियम लागू नहीं होते और उनके स्थान पर आपेक्षिकता सिद्धांत के अनुसार प्राप्त हुए नियमों तथा फलों की आवश्यकता होती है। आपेक्षिकता सिद्धांत से भौतिकी में जो क्रांति हुई उसका यथार्थ ज्ञान होने के लिए केवल सामान्य गणित ही नहीं, किंतु उच्च गणित की आवश्यकता होती है, जिसमें दिक्‌ तथा काल की भी मिथ: क्रिया होती है। बिना पूरा गणित दिए विशिष्ट आपेक्षिकता सिद्धांत से प्राप्त हुए थोड़े से फल यहाँ दिए जाते हैं:

आपेक्षिकता और समक्षणिकता-निर्वात प्रदेशों में प्रकाश का वेग 3´1010 सेंटीमीटर प्रति सेकेंड होता है। प्रकाश के सब वर्णों के लिए यह वेग समान होता है। जिस स्थान या उद्गम से प्रकाश निकलता है उसके वेग पर प्रकाश का वेग अवलंबित नहीं होता। इस प्रकार प्रकाश का (तथा सब विद्युच्चुंबकीय तरंगों का) वेग निर्वात में उतना ही रहता है। प्रकाश के इस गुण के परिणाम महत्वपूर्ण होते हैं। उदाहरणत:, हम कल्पना करेंगे कि एक प्रेक्षक पृथ्वी पर खड़ा है और उसके ऊपर से एक विमान पश्चिम से आकर पूर्व दिशा की ओर वेग व से जा रहा है। जिस समय विमान प्रेक्षक के मस्तक के ऊपर आता है ठीक उसी समय प्रेक्षक के समान अंतर पर दो विद्युत्‌ की बत्तियाँ जला दी गई, जिनमें एक बत्ती पूर्व दिशा में दूरी द पर है और दूसरी पश्चिम दिशा में दूरी द पर ही है। पृथ्वी पर स्थित प्रेक्षक के लिए दोनों बत्तियों का जलना समक्षणिक (एक ही क्षण पर होनेवाला) दिखाई पड़ेगा, किंतु विमान में भी यदि कोई प्रेक्षक हो, तो उसके लिए दोनों बत्तियों का जलना समक्षणिक नहीं दिखाई पड़ेगा। क्योंकि विमान पूर्व दिशा की ओर वेग व से जा रहा है, इसीलिए पूर्व दिशावाली बत्ती का प्रकाश पहले दिखाई पड़ेगा और पश्चिम दिशा की बत्ती का प्रकाश कुछ क्षण बाद दिखाई पड़ेगा। इसका अर्थ यह है कि एक घटना किसी प्रेक्षक के लिए समक्षणिक हो तो उसके सापेक्ष गतियुक्त अन्य प्रेक्षक के लिए वही घटना समक्षणिक नहीं रहेगी। अत: समक्षणिकता निरपेक्ष नहीं, किंतु आपेक्षिक है। इस परिणाम को व्यापक रूप से देखने पर हम यह निष्कर्ष निकाल सकते हैं कि समय भी निरपेक्ष नहीं है, प्रत्युत प्रत्येक निर्देशपिंड के लिए अपनी अपनी स्वतंत्र समयगणना होती है, और दो निर्देशपिंडो पर, जो एक दूसरे के सापेक्ष एक समान (यूनिफ़ॉर्म) वेग से गतिमान हों, समयगणनाएँ भिन्न होंगी। इन दोनों समयगणनाओं के परस्पर संबंध से आपेक्षिक वेग व का भी संबंध होगा। अत: समय के विषय में हमारी जो व्यावहारिक धारणा है उसमें सापेक्षिकता सिद्धांत के अनुसार परिवर्तन करना पड़ेगा।

आपेक्षिकता और लंबाई तथा समय-(1) आपेक्षिकता सिद्धांत के अनुसार 'निरपेक्ष' गति का यदि अस्तित्व नहीं है, तो 'निरपेक्ष' विश्रांति का भी अस्तित्व नहीं है। भौतिकी में मापन करने के लिए पहले किसी एक मानक की आवश्यकता होती है और उस मानक का निर्देश करके मापन किए जाते हैं। स्वेच्छा से हम किसी एक परिस्थिति को प्रामाणिक समझ सकते हैं। स्वेच्छा से हम किसी एक परिस्थिति को प्रामाणिक समझ सकते हैं। अब हम यह कल्पना करेंगे कि एक विमान पृथ्वी से एक विशेष ऊँचाई पर रुका है और उसमें लंबाई ल का एक दंड है, अर्थात्‌ इस दंड की लंबाई का यथार्थ मापन एक मापनी की सहायता से हो सकता है। अब यदि वह विमान वेग व से जाने लगे तो आपेक्षिकता सिद्धांत के अनुसार उस दंड की माप में कितना परिवर्तन होगा? इस फल को प्राप्त करने के लिए हम दो प्रेक्षकों की कल्पना करेंगे। एक प्रेक्षक क विमान में बैठा है; अत: उसका वेग पृथ्वी के सापेक्ष व है, किंतु विमान के सापेक्ष शून्य है। दूसरा प्रेक्षक ख पृथ्वी पर (विमान के पूर्व स्थान पर) खड़ा है, अर्थात्‌ पृथ्वी के सापेक्ष उसका वेग शून्य है। विमान का वेग व होने के कारण उसमें बैठे हुए प्रेक्षक क का तथा दंड का वेग प्रेक्षक ख के सापेक्ष व होगा। यदि जिस समय विमान निश्चल था उस समय दंड की लंबाई ल रही हो, तो प्रेक्षक क के लिए वह लंबाई सदा ल ही रहेगी, कारण, उसके सापेक्ष दंड सदा विश्रांति में ही रहेगा। किंतु प्रेक्षक ख के लिए दंड वेग व से गतियुक्त है। इसलिए आपेक्षिकता सिद्धांत के अनुसार उसकी लंबाई में परिवर्तन होगा और नवीन लंबाई ल Ö(1-व2/प्र2) होगी, जहाँ प्र2= प्रकाश की निर्वात में गति है, अर्थात क और ख प्रेक्षकों के लिए एक ही दंड की लंबाई भिन्न-भिन्न होगी।

लंबाई के विषय में आपेक्षिकता सिद्धांत का यह फल हम व्यापक रूप में निम्नलिखित प्रकार से व्यक्त कर सकते है : किसी दंड या पदार्थ की लंबाई मापने पर प्रयोग का जो फल आता है उसको हम लंबाई ल कहते हैं। भौतिकी की दृष्टि से वस्तुत: यह लंबाई ल यथार्थ नहीं है, वरन्‌ ल Ö(1-व2/प्र2) है, जहाँ व दंड की लंबाई की दिशा में प्रेक्षक का दंड के सापेक्ष वेग है। इसका अर्थ यह नहीं है कि उस दंड में आकुंचन हो रहा है। लंबाई उस दंड का मौलिक गुण नहीं है, वरन्‌ उस दंड के संबंध में हमारी एक धारणा है और इस धारणा को हम ल तथा व के एक फलन (फ़ंक़्शन) के रूप में व्यक्त करते हैं। जैसे जैसे व में वृद्धि होती है वैसे वैसे यह फलन घटता है। लंबाई की सर्वसाधारण परिभाषा यदि इस स्वरूप में दी जाए तो भौतिकी में प्रयोगों के फल समझने में कठिनाई नहीं रहती और माईकेलसन-मॉर्ले के प्रयोग का अथवा केन्नेडी-थॉर्नडाइक के प्रयोग का सरलता से अर्थ बताया जा सकता है।

भौतिकी में गणित की तरह ही स्थान अथवा वेग निश्चित करने के लिए कार्तिसीय (कार्टिसियन) निर्देशांक पद्धति का उपयोग किया जाता है। इस पद्धति में एक मूल बिंदु म से तीन परस्पर लंब रेखाएँ खींची जाती हैं, जो अक्ष कहलाती हैं। प्रत्येक दो अक्षों से एक समतल मिलता है और बिंदु क की इन समतलों से दूरियाँ क के निर्देशांक होती हैं। यदि ये दूरियाँ य, र, ल हों तो कहा जाता है कि बिंदु क की स्थिति (य, र, ल,) है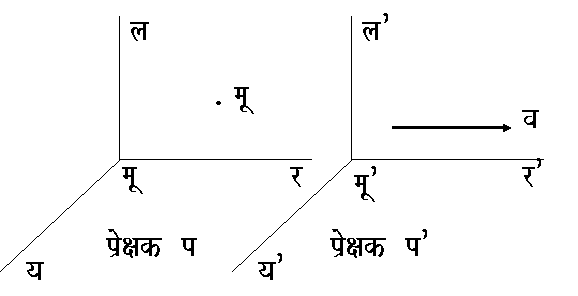

अब हम कल्पना करेंगे कि एक दूसरी ऐसी ही अक्ष पद्धति है, जिसके अक्ष पुराने अक्षों के समांतर हैं ओर उसके सापेक्ष ,य अक्ष के समांतर, एक समान वेग व से गतियुक्त हैं (चित्र 2)। यदि इन पद्धतियों में से प्रत्येक में प्रेक्षक हो, तो प्रेक्षक प' प्रेक्षक प के सापेक्ष वेग व से य अक्ष की दिशा में जा रहा है। मान लें किसी बिंदु क के निर्देशांक प्रेक्षक प की पद्धति में (य, र, ल) हैं और प्रेक्षक प की पद्धति में (य', र', ल')। यह भी मान लें कि जिस क्षण बिंदु मू' बिंदु मू पर था उस क्षण से समय की गणना का प्रारंभ हुआ। समय स के पश्चात्‌ मू से मू' की दूरी वस होगी। इसीलिए समय स पर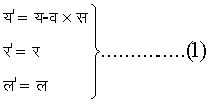
किंतु आपेक्षिकता सिद्धांत के अनुसार इस संबंध में परिवर्तन करना पड़ता है। निर्देशांक मापन में जिस एक का हम पद्धति प में उपयोग करेंगे उसकी लंबाई केवल य की दिशा में पद्धति प' में Ö(1-व2/प्र2) होगी। इसलिए पूर्वाक्त समीकरणों के बदले निम्नलिखित समीकरण ठीक होंगे :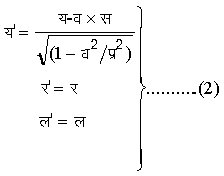

समीकरण (2) को 'रूपांतरण समीकरण' कहते हैं।

(2) समय को गणना करने के जो उपकरण होते हैं उनमें यांत्रिकी के साधनों का उपयोग किया जाता है और प्रत्यक्ष अथवा अप्रत्यक्ष रीति से हमारी समयगणना दिक्‌ अथवा लंबाई की गणना पर अवलंबित रहती है। अत: आपेक्षिकता सिद्धांत के अनुसार यदि लंबाई के मापन में वेग के कारण परिवर्तन होता है तो वेग के कारण समय के मापन में भी परिवर्तन होना आवश्यक है।

ऊपर निर्दिष्ट रूतांतरण समीकरण (2) केवल क्षणिक बिंदुओं के लिए यथार्थ होते हैं, किंतु किसी भी स्थान के लिए समय से स्वतंत्र नहीं होते। इसका अर्थ यह हुआ कि इन समीकरणों में जो समय का क्षण स आता है उसका वास्तविक स्वरूप एक निर्देशांक जैसा है। किसी स्थान को निश्चित करने के लिए जिस प्रकार (य,र,ल) इन तीन निर्देशांको की आवश्यकता होती है; उसी प्रकार किसी घटना को निश्चित करने के लिए समय की आवश्यकता होती है। अत: इन तीन निर्देशांकों के साथ समय स भी युक्त करना पड़ेगा। यदि पद्धति प मे किसी घटना के निर्देशांक (य,र,ल,स) हों तो पद्धति प' में उनके संगत निर्देशांक (य',र',र',स') होंगें जिनमें क्रमानुसार य',र',ल', के य, र, ल से संबंध समीकरण (2) द्वारा प्राप्त होते हैं। स तथा स' का परस्पर संबंध निकालने के लिए पुन: आपेक्षिकता सिद्धांत की सहायता लेनी होगी। माइकेलसन-मॉर्ले के प्रयोग का फल मूलभूत समझकर चलना अधिक सरल होगा। माइकेलसन-मॉर्ले के प्रयोग के अनुसार प्रकाश की गति सर्वनिर्देशांक पद्धतियों में (उदाहरणार्थ पूवोक्त पद्धतियों प, प' में) समान होती है।

हम कल्पना करेंगे कि समय स= 0 पर मू तथा मू' (चित्र1) अभिन्न थे और ठीक उसी समय पर प्रकाश की एक किरण य-अक्ष की दिशा में निकलती है। पद्धति प' पद्धति प के सापेक्ष य-अक्ष की दिशा में समान वेग व से जा रही है, अत: कुछ समय पश्चात्‌ यह किरण जिस स्थान पर पहुँचेगी उसके निर्देशांक इस प्रकार के होंगे:

पद्धति प' में :(य',र',ल') समय स' के पश्चात्‌।

पद्धति प में : (य, र, ल) समय स के पश्चात्‌।

माइकेलसन-मोर्ले के प्रयोगानुसार इन दोनों पद्धतियों में प्रकाश का वेग समान होगा। अत:

इस समीकरण में स तथा स' का जो परस्पर संबंध निश्चित होता है उसमें व भी आता है। अब समीकरण (2) तथा (3) को एकत्रित करने से, दिक्‌ के तीन निर्देशांक और समय, इन चारों, इन चारों, कें संबंध के लिए निम्नलिखित चार समीकरण मिलते हैं :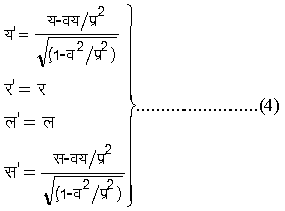

समीकरण (4) को लोरेंट्ज़ का रूपांतरण समीकरण अथवा सूत्र कहते हैं लोरेंट्स के समीकरण आपेक्षिकता सिद्धांत के पहले ही प्राप्त किए गए थे, किंतु उनका पूरा महत्व उस समय लोगों ने नहीं समझा था।

(3) लोरेंट्ज़ के रूपांतरण समीकरणों से डालप्लर परिणाम (डॉप्लर एफ़ेक्ट), प्रकाशविपथन इत्यादि अन्य फल प्रमाणित किए जा सकते हैं। फिर फ़ीजों ने प्रवाहित पानी में प्रकाश का जो वेग प्रयोग से नापा था, उसके मान का समर्थन आपेक्षिकता सिद्धांत से सरलता से होता है। वेग तथा त्वरण के लिए भी रूपांतरण सूत्रों की आवश्यकता होती है। लारेंट्ज़ के रूपांतरण समीकरणों से ये सूत्र सरलता से प्राप्त हो सकते हैं।

आपेक्षिकता सिद्धांत में द्रव्यमान तथा ऊर्जा-याँत्रिकी में आपेक्षिकता सिद्धांत का उपयोग करने से एक और महत्वपूर्ण फल मिलता है। दिक्‌ तथा समय के साथ-साथ भौतिकी में द्रव्यमान का भी महत्वपूर्ण स्थान है। वेग तथा समय आपेक्षिक हैं और उनके संबंध समीकरण (4) से प्राप्त होते हैं। आपेक्षिकता सिद्धांत के मूल तत्वों का याँत्रिकी में उपयोग करने से (विशेषत: ऐसे प्रयोगों में जहाँ द्रव्यमान का संबंध आता है-उदाहरणार्थ, दो आदर्श प्रत्यास्थ गोलों के संघात में) यह फल प्राप्त होता है कि जैसे लंबाई वेग पर निर्भर है वैसे ही द्रव्यमान भी वेग पर निर्भर है। किसी एक निर्देशपद्धति के सापेक्ष विश्रांपि स्थिति में एक पिंड का द्रव्यमान यदि म. हो, तो जब पिंड वेग व से चलता रहता है जब उसके द्रव्यमान में निम्नलिखित समीकरण के अनुसार वृद्धि होती है 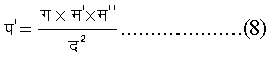समीकरण (5) से यह स्पष्ट है कि द्रव्यमान पिंड का अचर गुण नहीं है, क्योंकि उसमें वेग के अनुसार परिवर्तन होता है। आपेक्षिकता सिद्धांत के पहले द्रव्यमान के विषय में जो धारणा थी उसमें गंभीरता से विचार करने की आवश्यकता समीकरण (5) से उत्पन्न हुई।

इस विचारधारा को आगे बढ़ाने से द्रव्यमान तथा ऊर्जा के संबंध में भी विलक्षण परिणाम मिलता है। याँत्रिकी के अनुसार यदि म द्रव्यमान का पिंड व वेग से गतियुक्त हो तो उसकी गतिज ऊर्जा 1/2 मव2 होती है। आपेक्षिकता सिद्धांत के अनुसार वेग के कारण द्रव्यमान में वद्धि होती है और साथ-साथ समानुपाती गतिज ऊर्जा भी प्राप्त होती है। इस धारणा को गणित की सहायता से विस्तृत करने पर यह फल प्राप्त होता है कि जिस पिंड का द्रव्यमान म है उसकी संपूर्ण ऊर्जा म´प्र2 होती है, अर्थात

ऊ= म.प्र2

[E=mc2]

द्रव्यमान तथा ऊर्जा का परस्पर संबंध समीकरण (6) से स्पष्ट होता है। अत: द्रव्यमान तथा ऊर्जा ये एक ही वस्तु के केवल दो विभिन्न स्वरूप हैं और द्रव्यमान का ऊर्जा में अथवा ऊर्जा का द्रव्यमान में परिवर्तन हो सकता है। किसी पदार्थ से ऊर्जा का विकिरण होता हो तो समीकरण (6) के अनुरूप उसका द्रव्यमान घटता जायगा (उदाहरणार्थ सूर्य का)। किसी भौतिक घटना में केवल द्रव्यमान की अविनाशिता अथवा केवल ऊर्जा की अविनाशिता मानना अपूर्ण होगा, किंतु समीकरण (6) का उपयोग करके घटना के पूर्व और घटना के पश्चात उसकी संपूर्ण ऊर्जा अथवा संपूर्ण द्रव्यमान अविनाशिता के नियम के अनुसार समान रहेगा।

द्रव्यमान में वेग के कारण जो परिवर्तन होता है वह सामान्य वेगों के लिए अत्यंत उपेक्षणीय होता है; अत: नित्य व्यवहार में यह परिवर्तन अनुभव में नहीं आता है। ऊर्जा तथा द्रव्यमान की समानता भी नित्य व्यवहार के लिए निरुपयोगी है। जहाँ विशाल वेगों का संबंध आता है, केवल वहीं समीकरण (5) और (6) का उपयोग हो सकता है। जब द्रव्यमान है में न्यूनता होती है तब समीकरण (6) के अनुसार इस नष्ट द्रव्यमान से इतनी प्रचंड ऊर्जा प्राप्त होती है कि अवशिष्ट द्रव्यमान को विशाल गति मिलती है (द्र.परमाण्वीय ऊर्जा)।

आपेक्षिकता सिद्धांत के परिणाम के प्रायोगिक तथा अन्य प्रमाण-माइकेलसन'मॉर्ले के प्रयोग के फल का आकलन तथा स्पष्टीकरण करने के लिए आपेक्षिकता सिद्धांत प्रस्तुत किया गया था। किंतु इस वाद को विस्तृत करने के पश्चात्‌ समीकरण (4)(5)एवं(6) के अनुसार जो अतिरिक्त फल मिलते हैं उनको प्रमाणित करने के लिए विशेष प्रयोगों की आवश्यकता थी। उपकरणों के निर्माण में जैसे-जैसे प्रगति हुई वैसे-वैसे यथार्थ मापन के लिए उचित उपकरण उपलब्ध होने लगे। ऐसे उपकरणों द्वारा किए गए प्रयोगों से समीकरण (4),(5) और (6) यथार्थता से प्रमाणित हुए और आपेक्षिकता सिद्धांत को अधिक पुष्टि मिली। भौतिकी में, विशेषत: नाभिकीय भौतिकी में, कतिपय प्रयोगों के फल आपेक्षिकता सिद्धांत के दृष्टिकोण से ही संतुष्ट होते हैं। आपेक्षिकता सिद्धांत के अपवाद का एक भी उदाहरण वर्तमान काल तक भौतिकी में नहीं मिला है। केवल डी.सी. मिलर के प्रयोगों में ईथर के सापेक्ष पृथ्वी की गति का आभास मिलता है। ये प्रयोग माइकेलसन-मोर्ले के प्रयोग के समान थे। परंतु मिलर के प्रयोग के फल वैज्ञानिकों में सर्वमान्य नहीं है।

समीकरण (4) के अनुसार लंबाई तथा समय दोनों वेगसंबद्ध हैं। इन समीकरणों का प्रत्यक्ष फल नापने के लिए वेग व प्रकाश के वेग प्र से तुलनीय होना चाहिए। जैसा पहले बताया गया है, व्यवहार के सामान्य वेगों के लिए लंबाई तथा समय में जो परिवर्तन होता है वह उपेक्षणीय है। परमाणु भौतिकी में आधुनिक काल में जो प्रगति हुई और प्रचंड ऊर्जा प्राप्त करने का आविष्कार हुआ, उनकी सहायता से प्र से तुलनीय वेग प्रयोगशाला में अब मिल सकता है। इसी प्रकार पृथ्वी पर अंतरिक्ष किरणों (कॉस्मिक रेज़) की जो वर्षा होती है, उसमें प्रचंड वेग तथा ऊर्जा के कण होते हैं। इनमें एक विशेष प्रकार के कण, मेसान, होते हैं। जो आकाश में पृथ्वी से 10 किलोमीटर की ऊँचाई पर निर्मित होते हैं। इनका जीवनकाल लगभग 3´10-6 सेकेंड होता है। सामान्य गणना के अनुसार पृथ्वी पर पहुँचने के लिए इनका वेग प्र से बहुत अधिक होगा, किंतु विशिष्ट आपेक्षिकता सिद्धांत के अनुसार यह असंभव है। यदि विशिष्ट आपेक्षिकता सिद्धांत का यहाँ उपयोग किया जाय तो यह जीवनकाल प्रत्येक मेसान के साथ उसके ही वेग से चलनेवाली घड़ी का समय है। पृथ्वी पर के प्रेक्षक के लिए यह घड़ी विलम्बित (मंद गति) चलेगी। अत: समय के सूत्र में उचित संशोधन करने पर इन मेसानों का वेग 0.99 प्र आता है और जीवनकाल भी ठीक आता है। द्रव्यमान का वेग के ऊपर अवलंबन (समीकरण 5) तो अनेक प्रयोगों में प्रमाणित हुआ है। इलेक्ट्रान को प्रचंड विभव (पोटेंशियल) से त्वरित करने पर उसकी गति प्र से तुलनीय हो सकती है और उसका प्रत्यक्ष पथ निकालने के लिए उसके द्रव्यमान की गणना समीकरण (5) के अनुसार करनी पड़ती है। द्वितीय विश्वयुद्ध को जिसने शीघ्र समाप्त किया और वर्तमान काल में ऊर्जा का एक नवयुग प्रस्थापित किया, वह परमाणु बम ऊर्जा समीकरण (6) का ही फल है। यदि म ग्राम द्रव्यमान नष्ट हो तो मप्र अर्ग ऊर्जा मिलती है। यूरेनियम-235 का केवल 0.1 प्रतिशत द्रव्यमान नष्ट होने से परमाणु बम जैसा महास्त्र तैयार होता है (द्र.परमाण्वीय ऊर्जा) इससे अधिक द्रव्यमान नष्ट हो तो अधिक ऊर्जा प्राप्त होगी और अधिक शक्तिशाली महास्स्र प्राप्त होगा, उदाहरणत: हाइड्रोजन बम। जिस समय अति प्रचंड ताप में हाइड्रोजन के परमाणु एकत्रित होते हैं और हीलियम के नए परमाणु बनते हैं, उस समय अधिक द्रव्यमान नष्ट होने के कारण परमाणु बम से सहस्रगुनी अधिक ऊर्जा उत्पन्न होती है। सूर्य अनेक कोटि शताब्दियों से सतत प्रचंड उष्मा (ऊर्जा का ही एक स्वरूप) देता आ रहा है। सूर्य की इस शक्ति का रहस्य भी समीकरण (6) से स्पष्ट होता है। अत: भौतिकी की वर्तमान प्रगति से हम यह निश्चित रूप से कह सकते हैं कि विशिष्ट आपेक्षिकता सिद्धांत के सब फल प्रत्यक्ष अथवा अप्रत्यक्ष रीति से प्रमाणित हो चुके हैं और उनकी यथार्थता में कोई संदेह नहीं रहा है।

व्यापक आपेक्षिकता सिद्धांत (जनरल रिलेटिविटी थ्योरी)-व्यापक आपेक्षिकता सिद्धांत (1)आपेक्षिकता नियम और (2)गुरुत्वाकर्षणीय तथा जड़ता (इनर्शिया) पर आश्रित द्रव्यमानों की समानता, इन दो परिकल्पनाओं पर आधारित है। लंबाई, दिक्‌,काल, संहति, ऊर्जा इत्यादि के विषय में भोतिकी में जो धारणाएँ थीं उनमें विशिष्ट आपेक्षिकता सिद्धांत ने सुधार किया। इनके अतिरिक्त भौतिकी के क्षेत्र में अन्य विषय हैं जो उतने ही महत्वपूर्ण हैं, किंतु उनका समावेश विशिष्ट आपेक्षिकता सिद्धांत में नहीं है। बल तथा विद्युच्चुंबकीय क्षेत्रों में विशिष्ट आपेक्षिकता सिद्धांत का जैसा उपयोग हो सकता है जैसा गुरूत्वाकर्षणीय क्षेत्र में नहीं हो सकता। गुरूत्वाकर्षण भौतिकी का एक अत्यंत महत्वपूर्ण विभाग है, अत: विशिष्ट आपेक्षिकता सिद्धांत को व्यापक बनाने की आवश्यकता स्पष्ट है।

द्रव्यमान का संबंध भौतिकी में दो प्रकार से आता है। किसी पिंड पर जब बल कार्य करता है तब पिंड का स्थान बदलता है और उसका वेग बदलता है। जब तक बल कार्य करता है तब तक पिंड को त्वरण मिलता है। याँत्रिकी के नियमों के अनुसार बल (प), पिंड का द्रव्यमान (म) और त्वरण (फ) में निम्नलिखित संबंध है :

प=म´फ . . . (7)

समीकरण (7) में जो द्रव्यमान म है उसको जड़ता या आश्रित (अथवा अवस्थितित्वीय) द्रव्यमान कहते हैं। द्रव्यमान का दूसरा संबंध न्यूटन के गुरुत्वाकर्षणीय क्षेत्र में आता है। न्यूटन प्रणीत गुरुत्वाकर्षण के सिद्धांत के अनुसार यदि दो द्रव्यमान, म' तथा म, दूरी द पर हों, तो उनके बीच में निम्नलिखित गुरुत्वाकर्षणीय बल प' काम करेगा :

समीकरण (8) में ग गुरुत्वाकर्षण स्थिरांक है। यदि हम म' को पृथ्वी का द्रव्यमान समझें और म को समीकरण (7) में के किसी पिंड का द्रव्यमान समझें तो समीकरण (8) द्रव्यमान म का भार व्यक्त करेगा। न्यूटन की याँत्रिकी में गतिविज्ञान तथा गुरुत्वाकर्षण स्वतंत्र और भिन्न हैं, किंतु दोनों में ही द्रव्यमान का संबंध आता है। द्रव्यमान के इन दो स्वतंत्र तथा भिन्न विभागों में प्रयुक्त कल्पनाओं का एकीकरण आइंस्टाइन ने अपने व्यापक आपेक्षिकता सिद्धांत में किया। यह ज्ञात था कि जड़ता पर आश्रित द्रव्यमान (समीकरण 7) और गुरुत्वाकर्षणीय द्रव्यमान (समीकरण 8) समान होते हैं। आइंस्टाइन ने द्रव्यमान की इस समानता का उपयोग करके गतिविज्ञान और गुरुत्वाकर्षण को एकरूप किया और सन्‌ 1915 ई. में व्यापक आपेक्षिकता सिद्धांत प्रस्तुत किया।

व्यापक आपेक्षिकता सिद्धांत को गणित में सूत्रित करने की जो पद्धति है वह अन्य पद्धतियों से भिन्न है। इसमें विशेष ज्यामिति का उपभोग किया जाता है, जो यूक्लिड की त्रि-आयामीय ज्यामिति से भिन्न है। मिंकोव्स्की ने यह बताया कि यदि विशिष्ट आपेक्षिकता सिद्धांत में दिक्‌ के तीन आयाम तथा समय का चतुर्थ आयाम, इन चारों आयामों को लेकर एक 'चतुरायाम सतति' (फ़ोर डाइमेंशनल कॉन्टिनुअम), की कल्पना की जाए तो आपेक्षिकता सिद्धांत अधिक सरल हो जाता है। समक्षणिकता निरपेक्ष नहीं है, यह प्रमाणित किया जा चुका है। इससे न्यूटन प्रणीत दिक्‌ तथा समय की निरपेक्षता और स्वतंत्रता समाप्त हो जाती है। अत: भौतिक घटना व्यक्त करने के लिए दिक्‌ तथा समय की चतुरायाम सतति अधिक स्वाभाविक है। रीमान ने 'चतुरायाम दिक्‌' की कल्पना करके उसकी ज्यामिति का जो विकास किया था उसका आइंस्टाइन ने अधिक उपयोग किया। दिक्‌ तथा समय की इस चतुरायाम सतति में भौमिकी के सिद्धांत ज्यामितीय रूप से व्यापक आपेक्षिकता सिद्धांत में रखे गए। इस चतुरायाम सतति का (अथवा 'विश्व' का) युक्लिड के तीन आयाम के दिक्‌ से साम्य है। तीन आयाम की सतति में (य, र, ल) इन तीन निर्देशांकों से (अथवा आयामों से) जिस प्रकार बिंदु अथवा एक स्थान निश्चित होता है, वैसे ही दो बिंदु (य1, र1, ल1) और (य2, र2, ल2) के बीच की लंबाई भी निश्चित होती है। चतुरायाम सतति में दिक्‌ के (य, र, ल) इन तीन आयामों के साथ जब समय भी जोड़ा जाता है तब समय का आयाम रूप Ö(-1) स प्र आता है, जहाँ स=समय और प्र=प्रकाश का वेग है। एक प्रेक्षक के लिए एक विश्वघटना के निर्देंशांक (य, र, ल, स) हों तो उस प्रेक्षक के सापेक्ष गतिमान दूसरे प्रेक्षक के लिए उसी घटना के निर्देशंक (य', र', ल', स') होंगे। लोरेंट्ज़ के रूपांतरणा नियम यदि यथार्थ हों तो सिद्ध किया जा सकता है कि (9). समीकरण (9) में चतुर्थ निर्देशांक Ö(-1) प्रस, आता है जिसमें Ö(-1) काल्पनिक संख्या है।

समीकरण (9) का विकास करके किसी भी प्रकार की गति के लिए इसी प्रकारकी किंतु अत्यधिक संमिश्र पदसंहतियाँ मिलती हैं। इसके लिए निश्चलों (इन्वैरिएँट्स) और आतानकों (टेन्सर्स) के सिद्धांतों की आवश्यकता होती है। मौलिक कल्पनाओं का इस रीति से विस्तार करने पर व्यापक आपेक्षिकता सिद्धांत में गुरुत्वाकर्षण स्वभावत: आता है। उसके लिए विशिष्ट परिकल्पनाओं की आवश्यकता नहीं हाती है।

व्यापक आपेक्षिकता सिद्धांत के फलों का प्रमाण-अनेक घटनाओं के फल आइंस्टाइन प्रणीत व्यापक आपेक्षिकता सिद्धांत के अनुसार तथा न्यूटन प्रणीत प्रतिष्ठित याँत्रिकी के अनुसार समान ही होते हें। किंतु खगोलिकी में जब व्यापक आपेक्षिकता सिद्धांत का उपयोग किया गया तब तीन घटनाओं के फल प्रतिष्ठित याँत्रिकी के अनुसार निकले फलों से कुछ भिन्न रहे। इन फलों से व्यापक आपेक्षिकता सिद्धांत की कसौटी का काम ले सकते हैं। ये तीन फल इस प्रकार हैं:

(1) अनेक वर्षों से यह ज्ञात था कि बुध ग्रह की प्रत्यक्ष कक्षा न्यूटन के सिद्धांतों के अनुसार नहीं रहती। गणना के पश्चात्‌ यह प्रमाणित हुआ कि व्यापक आपेक्षिकता सिद्धांत के क्षेत्र समीकरणों के अनुसार बुध ग्रह की जो कक्षा आती है वह प्रेक्षित कक्षा के अनुरूप है। उसी प्रकार पृथ्वी की प्रत्यक्ष कक्षा भी न्यूटन के सिद्धांतों के अनुसार नहीं हैं, किंतु पृथ्वी की कक्षा में त्रुटि बुध ग्रह की कक्षा की त्रुटि से बहुत कम है। तो भी कहा जा सकता है कि पृथ्वी की कक्षा की गणना में व्यापक आपेक्षिकता सिद्धांत सफल रहा। अत: इस विशाल मापक्रमों की घटनाओं में जहाँ प्रतिष्ठित याँत्रिकी असफल थी वहाँ व्यापक आपेक्षिकता सिद्धांत सफल रहा।

(2) व्यापक आपेक्षिकता सिद्धांत की दूसरी कसौटी प्रकाश की वक्रीयता है। प्रकाश की किरणें जब तीव्र गुरुत्वाकर्षण क्षेत्र में से होकर जाती हैं, तब व्यापक आपेक्षिकता सिद्धांत के अनुसार उनका पथ अल्प मात्रा में वक्र हो जाता है। प्रकाश ऊर्जा का ही एक स्वरूप है। अत: ऊर्जा एवं द्रव्यमान के संबंध के अनुसर (समीकरण 6) प्रकाश में भी द्रव्यमान होता है और द्रव्यमान को आकर्षित करना गुरुत्वाकर्षण क्षेत्र का गुण होने के कारण प्रकाशकिरण का पथ ऐसी स्थिति में स्वल्प मात्रा में टेढ़ा हो जाता है। इस फल की परीक्षा केवल सर्वसूर्यग्रहण के समय हो सकती है। किसी तारे का प्रकाश सूर्य के निकट से होकर निकले तो प्रकाश के मार्ग को अल्प मात्रा में वक्र हो जाना चाहिए और इसलिए तारे की आभासी स्थिति बदल जानी चाहिए। व्यापक आपेक्षिकता के इस फल को नापने का प्रयत्न 1919, 1922, 1927, 1947 इत्यादि वर्षों में सर्व सूर्यग्रहण के समय किया गया। पता चला कि प्रकाशकिरण के पथ की मापित वक्रता और व्यापक आपेक्षिकता सिद्धांत के अनुसार निकली वक्रता में इतना सूक्ष्म अंतर है कि हम यह कह सकते हैं कि ये प्रेक्षण व्यापक आपेक्षिकता सिद्धांत का समर्थन करते हैं।

(3) व्यापक आपेक्षिकता सिद्धांत की तीसरी परीक्षा गुरुत्वाकर्षणीय क्षेत्र के कारण वर्ण-क्रम-रेखाओं (स्पेक्ट्रॉस्कोपिक लाइंस) का स्थानांतरण है। इस वाद के अनुसार जो तारे तीव्र गुरुत्वाकर्षणीय क्षेत्र में हैं उनके किसी विशेष तत्व के परमाणुओं से निकले प्रकाश का तरंगदैर्ध्य पृथ्वी के उसी तत्व के परमाणुओं के प्रकाश-तरंग-दैर्ध्य से अधिक होगा। अत: तारे के किसी एक तत्व के प्रकाश के वर्णक्रम और प्रयोगशाला में प्राप्त उसी तत्व के वर्णक्रम की तुलना से तरंगदैर्ध्य के परिवर्तन का मापन हो सकता है। अनेक निरीक्षणों के फल व्यापक आपेक्षिकता सिद्धांत के अनुरूप हैं, यद्यपि कुछ प्रक्षकों (फ्ऱाएँडलिख़ आदि) के अनुसार सब फल व्यापक आपेक्षिकता सिद्धांत के अनुरूप नहीं हैं।

आपेक्षिकता सिद्धांत और गुरुत्वाकर्षण-आपेक्षिकता के सिद्धांत के अनुसार यह विचार कि भौतिक वस्तुएँ एक दूसर को आकर्षित करती हैं, एक भ्रम है, जो प्रकृति संबंधी गलत याँत्रिक धारणाओं के कारण पैदा हुआ है। वस्तुत: गुरुत्वाकर्षण जड़ता का एक भाग मात्र है, तारे और ग्रहों की गतिविधियाँ, उनकी स्वभावगत जड़ता (इनर्शिया) से उत्पन्न होती है और उनका मार्ग दिक्‌-काल-सतति (स्पेस-टाइम-कॉन्टिनुअम) के वृत्तीय तत्वों पर निर्भर करता है। जिस प्रकार चुंबक के चारों ओर चुंबकीय क्षेत्र होता है उसी प्रकार खगोलीय वस्तु अपने चारों ओर के आकाश में एक क्षेत्र बिखेरती है। जिस तरह चुंबकीय क्षेत्र में एक लोहे के टुकड़े की गतिविधि क्षेत्र की बनावट से निर्देशित होती है उसी तरह गुरुत्वीय क्षेत्र में किसी वस्तु का मार्ग उस क्षेत्र की ज्यामितिक अवस्था से निर्धारित होता है।

आइंस्टाइन का गुरुत्वाकर्षण संबंधी नियम दिक्काल सतति के क्षेत्रीय तत्वों की जानकारी देता है। मुख्यत: इस नियम का एक भाग गुरुत्वाकर्षणजन्य वस्तु के चारों ओर के क्षेत्र के ढांचे से संबंध व्यक्त करता है।

आपेक्षिकता के सिद्धांत में प्रगति-आपेक्षिकता के सिद्धांत के प्रतिपादन के बाद भी इसमें कुछ प्रगतियाँ हुई हैं। इनमें से एक तथाकथित 'ब्रह्मांड-रचना-समस्या' के संबंध में है। आपेक्षिकता के सिद्धांत से पहले ऐसा समझा जाता था कि दिक्रूपी अगाध सागर में ब्रह्मांड तैरते हुए एक द्वीप के समान है। लेकिन अचल तारों के प्रेक्षण से यह स्पष्ट हो गया है कि ब्रह्मांड अनंत रिक्ताकाश (दिक्रूपी अगाध सागर) में तैरते हुए द्वीप के सदृश नहीं है और जितना द्रव्य ब्रह्मांड में विद्यमान है उस सब के लिए गुरुत्वकेंद्र (सेंटर ऑव ग्रैविटी) जैसे किसी बिंदु का अस्तित्व नहीं है। आपेक्षिकता के सिद्धांत के द्वारा ब्रह्मांड का जो रूप सामने आया उसकी तुलना साबुन के एक ऐसे बुलबुले से की गई है जिसकी सतह पर सिलवटें हों। अंतर इतना है कि साबुन के बुलबुले में केवल दो विस्तार होते हैं जबकि ब्रह्मांडीय बुलबुले के चार विस्तार हैं-तीन दिक्‌ (स्पेस) के और एक काल का। शून्य दिक्‌ (जो कि शून्य काल से संयुक्त है) से इस बुलबुले का जन्म होता है।

आपेक्षिकता के सिद्धांत के अनुसार ब्रह्मांड अनंत है और वह अनंत पर युक्लिडीय है। ब्रह्मांड को सीमित मान लेने पर भी उसका एक आयाम असीमित ही रहता है।

आपेक्षिकता के सिद्धांत की प्रगति का एक भाग यह भी है कि प्रकाश के उद्गम के (ऋणात्मक) गुरुत्वीय विभव के कारण होनेवाले स्पेक्ट्रमीय रेखाओं के रक्त विस्थापन (रेड शिफ़्ट) का अस्तित्व प्रेक्षण द्वारा असंदिग्ध रूप से प्रमाणित हो गया है। इसका प्रमाण तथाकथित वामन तारों के आविष्कार से संभव हुआ है जिनका घनत्व जल के घनत्व से लगभग 10,000 गुना अधिक है। प्रेक्षित विस्थापन का मान भी अपेक्षित सीमाओं के भीतर पाया गया।

आपेक्षिकता के सिद्धांत के प्रारंभिक निर्माण के गुरुत्वाकर्षित कण की गति का नियम गुरुत्वीय क्षेत्र के नियम के अतिरिक्त एक स्वतत्र मौलिक संकल्पनाओं के रूप में माना गया था जिसके अनुसार गुरुत्वाकर्षित कण अल्पांतरी (जियोडेसिक) रेखा पर गमन करता है। लेकिन बाद में यह प्रमाणित हुआ कि गति के इस नियम का विशाल द्रव्यपुंजों के लिए व्यापकीकृत रूप भी केवल रिक्ताकाश के क्षेत्र समीकरणों में से ही किया जा सकता है जिसकी व्युत्पत्ति के अनुसार गति का यह नियम इस प्रतिबंध से गर्भित है कि जिन द्रव्यबिंदुओं से इस क्षेत्र की उत्पत्ति होती है उनसे बाहर कहीं भी क्षेत्रीय विचित्रताओं (सिंग्युलैरिटीज़) का अस्तित्व नहीं होना चाहिए।

आइंस्टाइन के विशिष्ट आपेक्षिकता सिद्धांत से प्राप्त कई परिणामों को अनेक प्रयोगों द्वारा परखा जा चुका है और उसकी सत्यता सिद्ध की जा चुकी है। प्रकाश से अधिक तीव्र गतिवाले कणों (टैक्यान) का अस्तित्व आइंस्टाइन के सिद्धांत को असत्य सिद्ध नहीं करता अपितु ऐसे कणों के अस्तित्व का संकेत देता है। इस बात से कई भौतिकज्ञों ने सहमति जताई है।

पन्ने की प्रगति अवस्था

आधार

प्रारम्भिक

माध्यमिक

पूर्णता

शोध